1 Visualisation using ggplot2

Let’s start with a motivating example.

1.1 Gapminder

Professor Hans Rosling has made a name for himself in the field of data visualisation with his groundbreaking Gapminder project.

For a slightly longer presentation, his TED talk on global development has been watched over 11 million times. If you have 20 minutes, it can be found here, and is well worth a watch!

More-or-less as I had finished the first version of these notes, the news broke that Professor Rosling had sadly passed away on 7th February 2017, aged 68. I hope you will find some time to explore the Gapminder website, and appreciate the immense contribution that he made to the world of public health and education. He presented a world-view based on facts and data. To this end he provided innovative and fascinating ways to explore and understand data, disseminated these findings with pathos and humour, and used this information to challenge many of our pre-conceptions about public health and the developing world. An obituary from the Guardian can be found here.

The Gapminder website provides really informative interactive visualisations for many fascinating data sets. In this pracical we will explore how to use R to try to recreate something similar to the types of visualisation that Gapminder provides, and see how high-end R packages—such as ggplot2—have been developed that provide a systematic and flexible way to generate complex plots / visualisations. Our aim for this workshop is to emulate the plot in Figure 1.1.

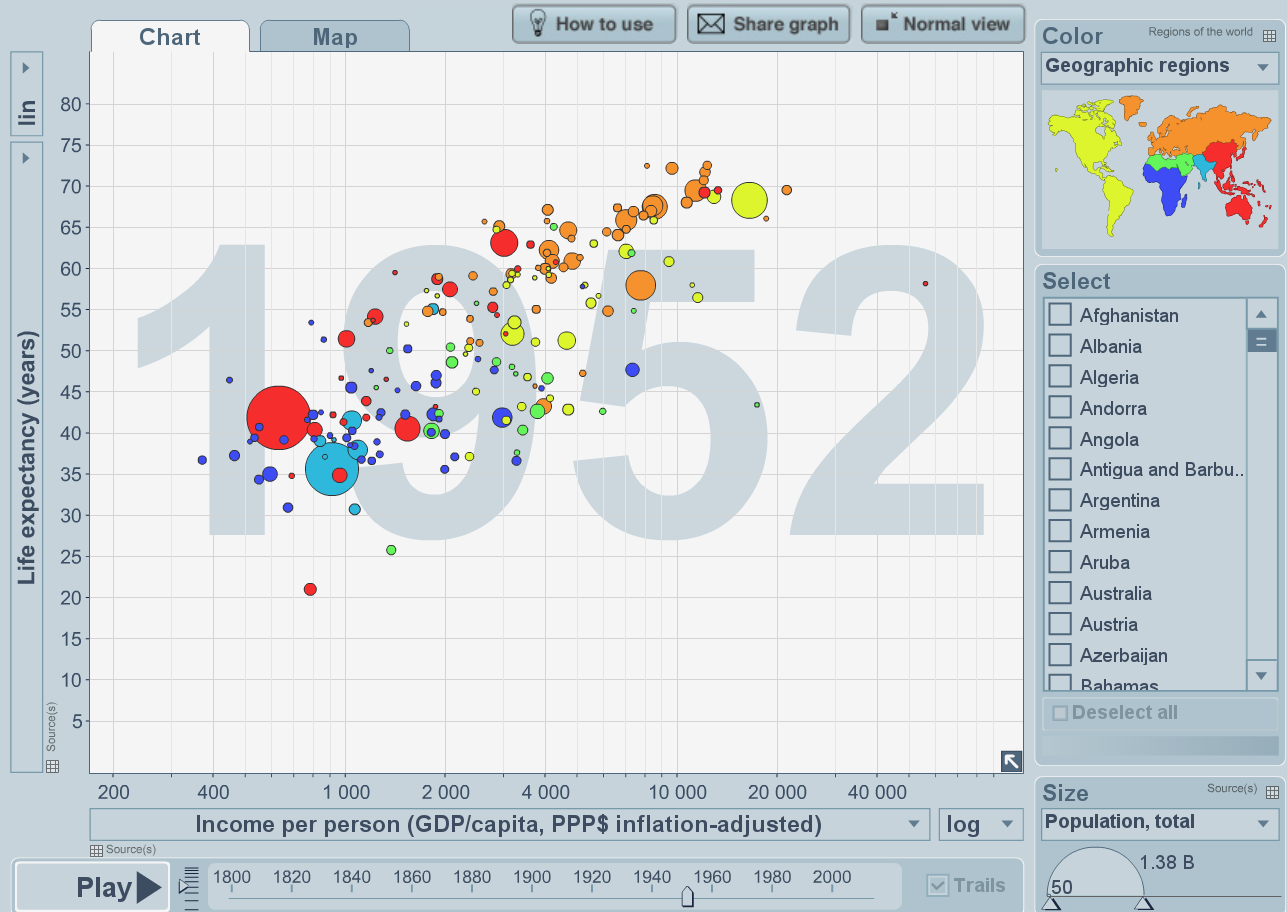
Figure 1.1: Life expectancy against GDP—screenshot from Gapminder project

Before we do this, let’s quickly remind ourselves of basic plotting functionality in R.

1.2 Base R graphics

Let’s begin by exploring the iris data set, which gives the measurements in centimeters of the variables sepal length and width, and petal length and width, respectively, for 50 flowers from each of 3 species of iris. The species are Iris setosa, versicolor, and virginica. This data set is available as part of the base R package. Let’s have a look at the data:

head(iris)

##   Sepal.Length Sepal.Width Petal.Length Petal.Width Species
## 1          5.1         3.5          1.4         0.2  setosa
## 2          4.9         3.0          1.4         0.2  setosa
## 3          4.7         3.2          1.3         0.2  setosa
## 4          4.6         3.1          1.5         0.2  setosa
## 5          5.0         3.6          1.4         0.2  setosa
## 6          5.4         3.9          1.7         0.4  setosa

Let’s start by visualising the variable Sepal.Lengthusing a kernel density plot:.

## kernel density of sepal length
plot(density(iris$Sepal.Length))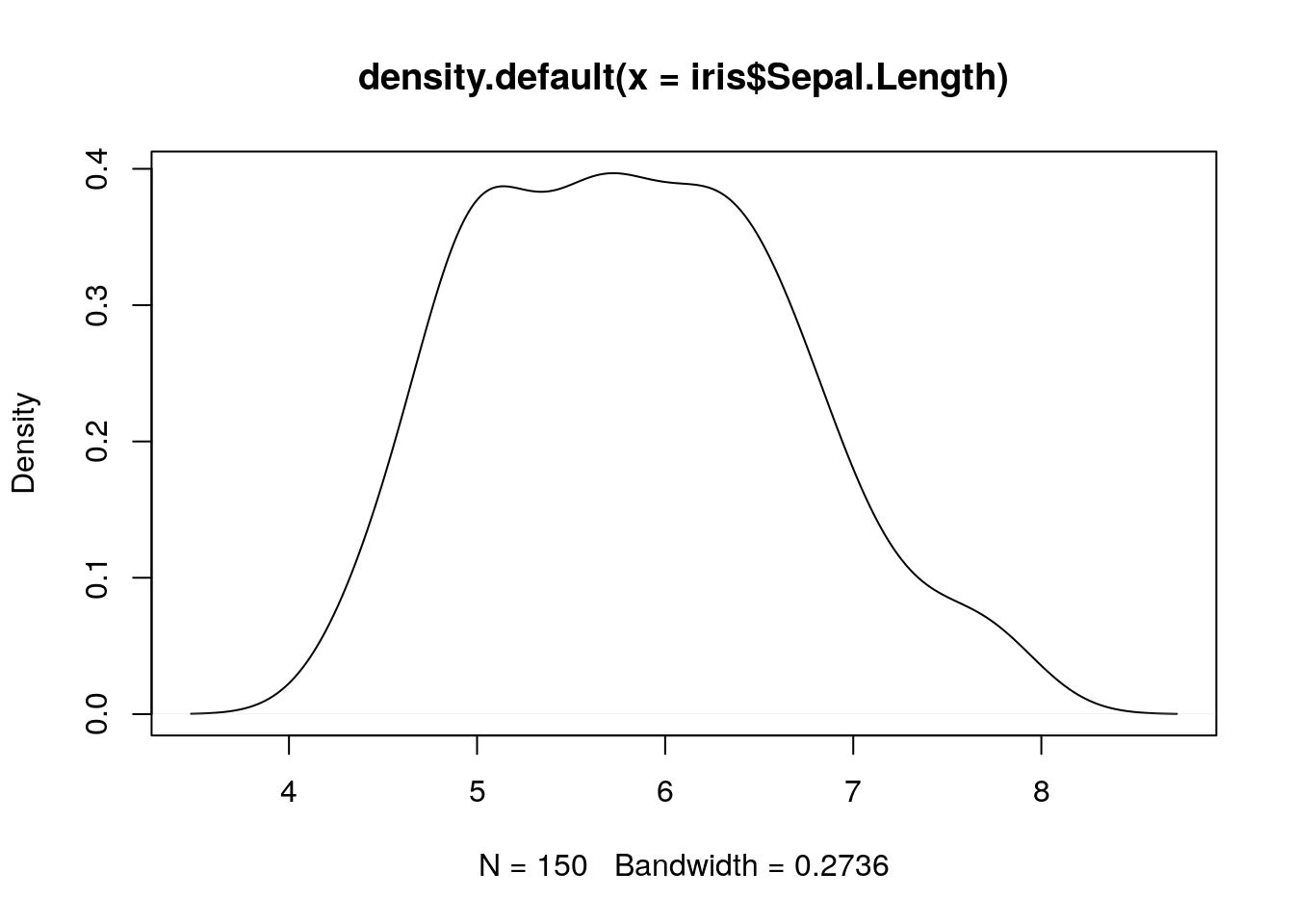

Remember that we can extract a named column from a data.frame using the $ operator. The density() function is a simple function in R that takes a vector argument and returns a kernel density object, which we can then plot using the generic plot() function.

Now let’s try to plot different kernel density plots for the three different species. We could do this as separate plots, and use our standard subsetting notation to extract the correct elements of the data frame in each case:

## plot Sepal.Length for setosa
plot(density(iris$Sepal.Length[iris$Species == "setosa"]))

## plot Sepal.Length for versicolor
plot(density(iris$Sepal.Length[iris$Species == "versicolor"]))

## plot Sepal.Length for virginica
plot(density(iris$Sepal.Length[iris$Species == "virginica"]))

What about if we want to add all three density lines to the same plot?

## place kernel density estimates on the same plot
plot(density(iris$Sepal.Length[iris$Species == "setosa"]), main = "")
lines(density(iris$Sepal.Length[iris$Species == "versicolor"]))
lines(density(iris$Sepal.Length[iris$Species == "virginica"]))

Notice the use of the lines() function to allow a line to be added to an existing plot.

Notice that the limits of the \(x\)- and \(y\)-axes in this case are set by the range of the initial setosa sepal lengths, and hence the density plots for the other two species extend beyond the plot window. Let’s try again, but this time setting the bounds for the plots manually. To do this we calculate the \(x\) and \(y\) ranges for each density plot separately, and then take the maximum values across the different species. We then use the xlim and ylim arguments to the plot() function in order to set the ranges:

## produce densities
setosa_dens <- density(iris$Sepal.Length[iris$Species == "setosa"])
versicolor_dens <- density(iris$Sepal.Length[iris$Species == "versicolor"])
virginica_dens <- density(iris$Sepal.Length[iris$Species == "virginica"])

## extract x-ranges and y-ranges
xlims <- range(c(setosa_dens$x, versicolor_dens$x, virginica_dens$x))
ylims <- range(c(setosa_dens$y, versicolor_dens$y, virginica_dens$y))

## produce plot
plot(density(iris$Sepal.Length[iris$Species == "setosa"]), 
     xlim = xlims, ylim = ylims, main = "")
lines(density(iris$Sepal.Length[iris$Species == "versicolor"]))
lines(density(iris$Sepal.Length[iris$Species == "virginica"]))

This is better, but still not very informative. Let’s add some colour and a legend, and tidy up the axis labels.

## produce plot
plot(density(iris$Sepal.Length[iris$Species == "setosa"]), 
    xlim = xlims, ylim = ylims, main = "", xlab = "Sepal Length (cm)")
lines(density(iris$Sepal.Length[iris$Species == "versicolor"]), col = "red")
lines(density(iris$Sepal.Length[iris$Species == "virginica"]), col = "blue")

## add legend to top-right corner
legend(par("usr")[2] * 0.8, par("usr")[4] * 0.95, 
       legend = c("setosa", "versicolor", "virginica"), 
       lty = c(1, 1, 1), 
       col = c("black", "red", "blue"))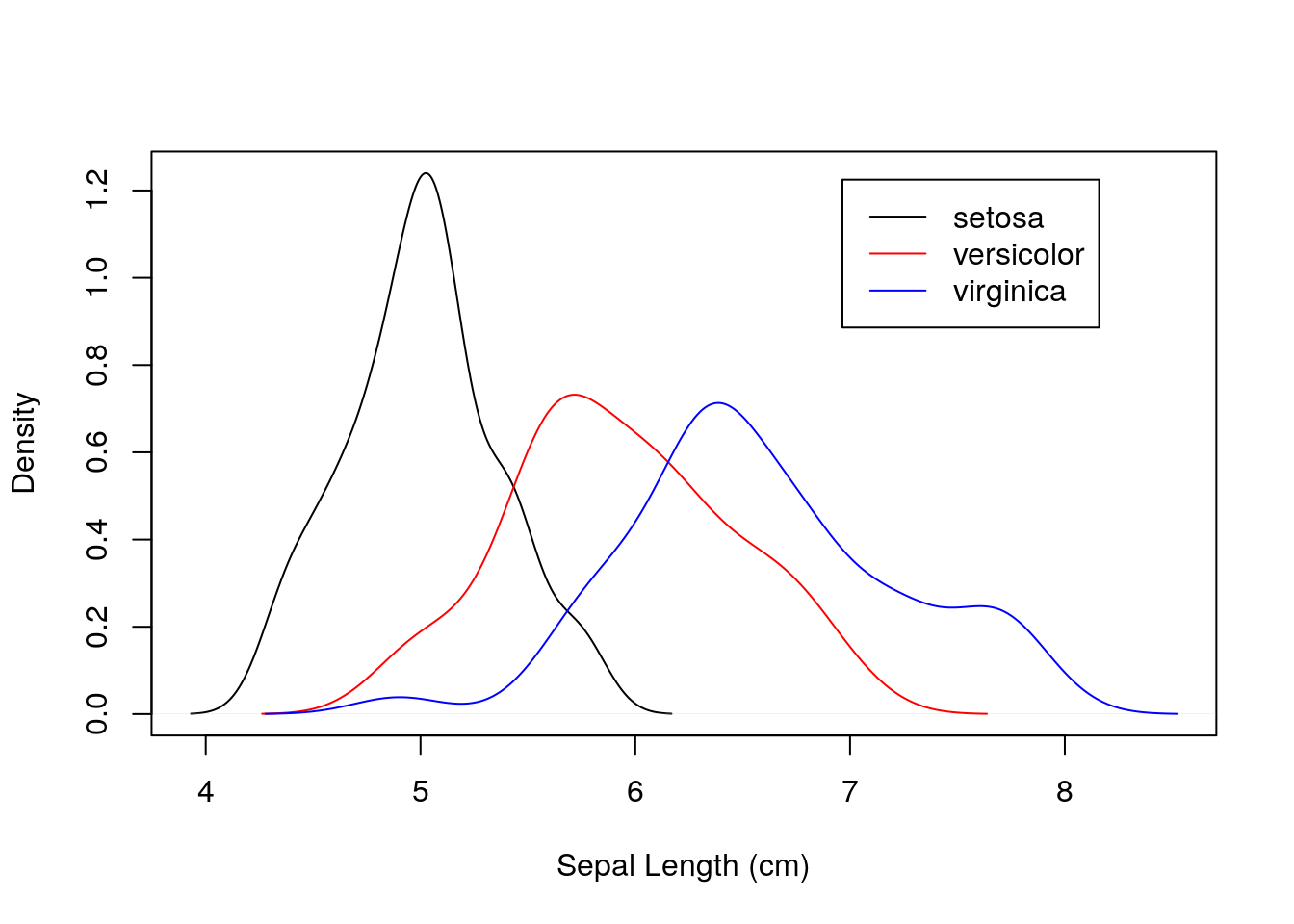

Notice that this is quite a simple plot, but required a series of steps to render in base R. We needed to calculate manual limits for the axes, plot the three species separately, and then add a custom legend to the plot.

Let’s look at another quick example. This time, let’s plot sepal length against sepal width for the three species.

## produce scatterplot
plot(iris$Sepal.Length, iris$Sepal.Width, 
     xlab = "Sepal Length (cm)", ylab = "Sepal Width (cm)")
points(iris$Sepal.Length[iris$Species == "versicolor"],
       iris$Sepal.Width[iris$Species == "versicolor"], col = "red")
points(iris$Sepal.Length[iris$Species == "virginica"],
       iris$Sepal.Width[iris$Species == "virginica"], col = "blue")

## add legend
legend(par("usr")[2] * 0.8, par("usr")[4] * 0.98, 
       legend = c("setosa", "versicolor", "virginica"), 
       pch = c(1, 1, 1), 
       col = c("black", "red", "blue"))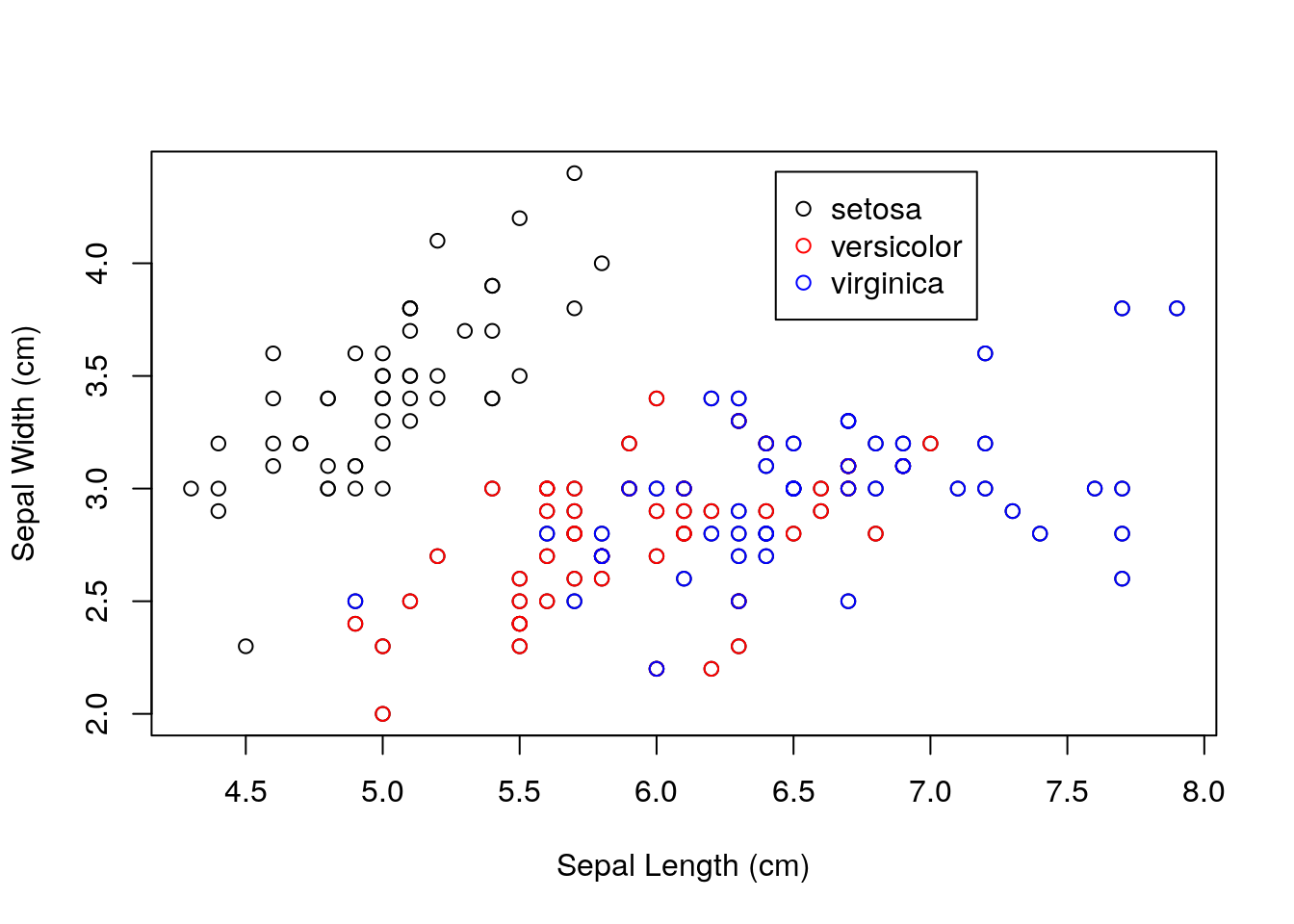

Notice the use of the points() function to add points to an existing plot. We could set the position of the legend manually, but the objects par("usr") provides the coordinates of the plot region in the form c(x1, x2, y1, y2), where x1 is the lower bound for the \(x\)-axis, and x2 is the upper bound for the \(x\)-axis, and similarly for y1 and y2.

1.3 Introduction to ggplot2

We have seen that the R base graphics system is highly flexible, and it can be used to produce high-quality, bespoke visualisations. However, doing so can be a lot of work! Let’s show an alternative way to produce similar plots using the ggplot2 package. We will introduce the code first, and then talk through it.

First we load the tidyverse (of which ggplot2 is included).

library(tidyverse)

Now run

ggplot(iris) +
    geom_point(aes(x = Sepal.Length, y = Sepal.Width, colour = Species))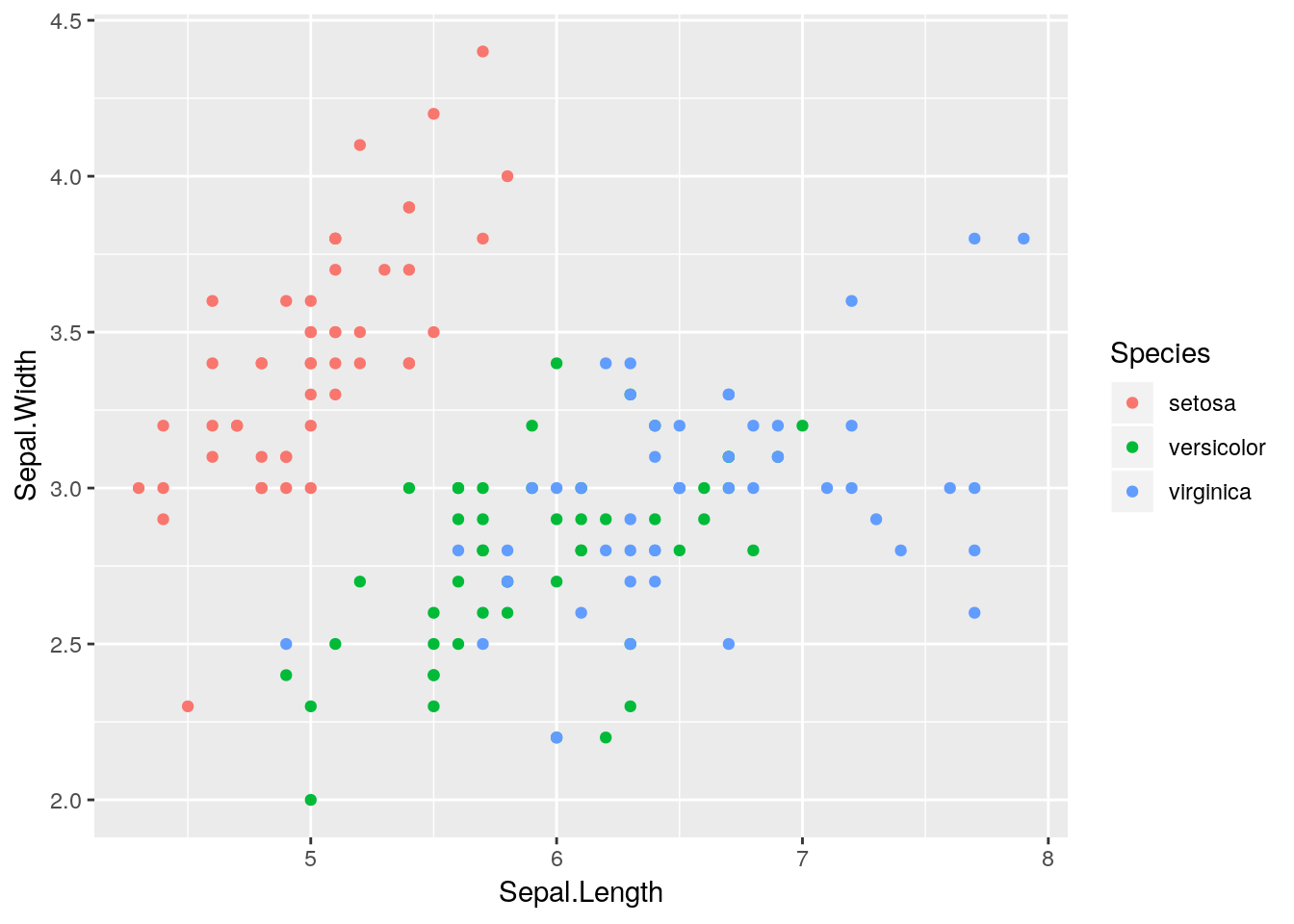

Notice that we had to do little physical manipulation of the plot. We didn’t have to choose how to position legends, or manually subset the data to plot the different points, or choose the colours; the package took care of all of these things.

So, how does it work? ggplot2 is based on a book called the Grammar of Graphics by Leland Wilkinson—hence the name gg-plot! The ethos of ggplot2 is that plots can be broken down into different features, most notably:

• data;
• aesthetic mapping;
• geometric object;
• scales;
• faceting;
• statistical transformations;
• coordinate system;
• position adjustments.

Perhaps the easiest way to explain some of these concepts is to work through our examples step-by-step. We will focus on the main components marked in bold above. Let’s start with the scatterplot example first, and examine the first part of the code:

ggplot(iris)

This sets up the plot. The first argument to the ggplot function is the data, which here is the iris data set.

Important: whereas base R graphics can plot various object types, ggplot() requires data.frame (or tibble¹) objects. It is designed for plotting statistical data sets. Never fear, most R objects can be manipulated into data.frames for plotting if required. (See next session on data wrangling.)

1.3.1 Aesthetics

The aes(x = Sepal.Length, y = Sepal.Width, colour = Species) part sets the aesthetics, which here are added as an argument to the geom_point() function (see nect section). These define how the data are mapped onto the visual aesthetics of the plot. Here we are setting the x coordinates to be Sepal.Length, the y coordinates to be Sepal.Width, and the colour of the characters to be related to Species. In general, aesthetics include:

• position;
• colour (border or line color);
• fill (inside color);
• shape;
• linetype;
• size.

As usual, information can be found in the relevant help files, but a really useful resource for ggplot2 is the Data Visualisation Cheat Sheet. Another fantastic resource, is the R Graphics Cookbook by Winston Chang, which has a free online version, or a physical book that you can buy.

Notice that we did not have to use the $ operator to extract columns. This makes ggplot2 code a lot clearer. R knows to look for the Sepal.Length and Sepal.Width columns in the iris data, because we have told ggplot() which data set to operate on.

1.3.2 Geoms

A geom defines the type of plot we want. In this case we want a scatterplot, which can be defined by the geom_point() function. Geoms can be layered, allowing us to built complex plots in different ways. Common geoms are:

• geom_point()
• geom_line()
• geom_histogram()
• geom_density()
• geom_bar()
• geom_violin()

Please see the Data Visualisation Cheat Sheet for more examples.

Note: ggplot2 builds plots up by adding together components. There are lots of ways to do this. Here I have set up “global” options for the plot using the ggplot() function. I then add (+) to this the type of plot I want i.e. + geom_point(aes(x = Sepal.Length, y = Sepal.Width, colour = Species)) (in this case including the aesthetics in the geom_* call). The addition sign is important. If I want to split the function over multiple lines, make sure the + sign is at the end of each line, so R knows that the plot is not complete at the point.

Let’s see how this works:

ggplot(iris) +
    geom_point(aes(x = Sepal.Length, y = Sepal.Width, colour = Species))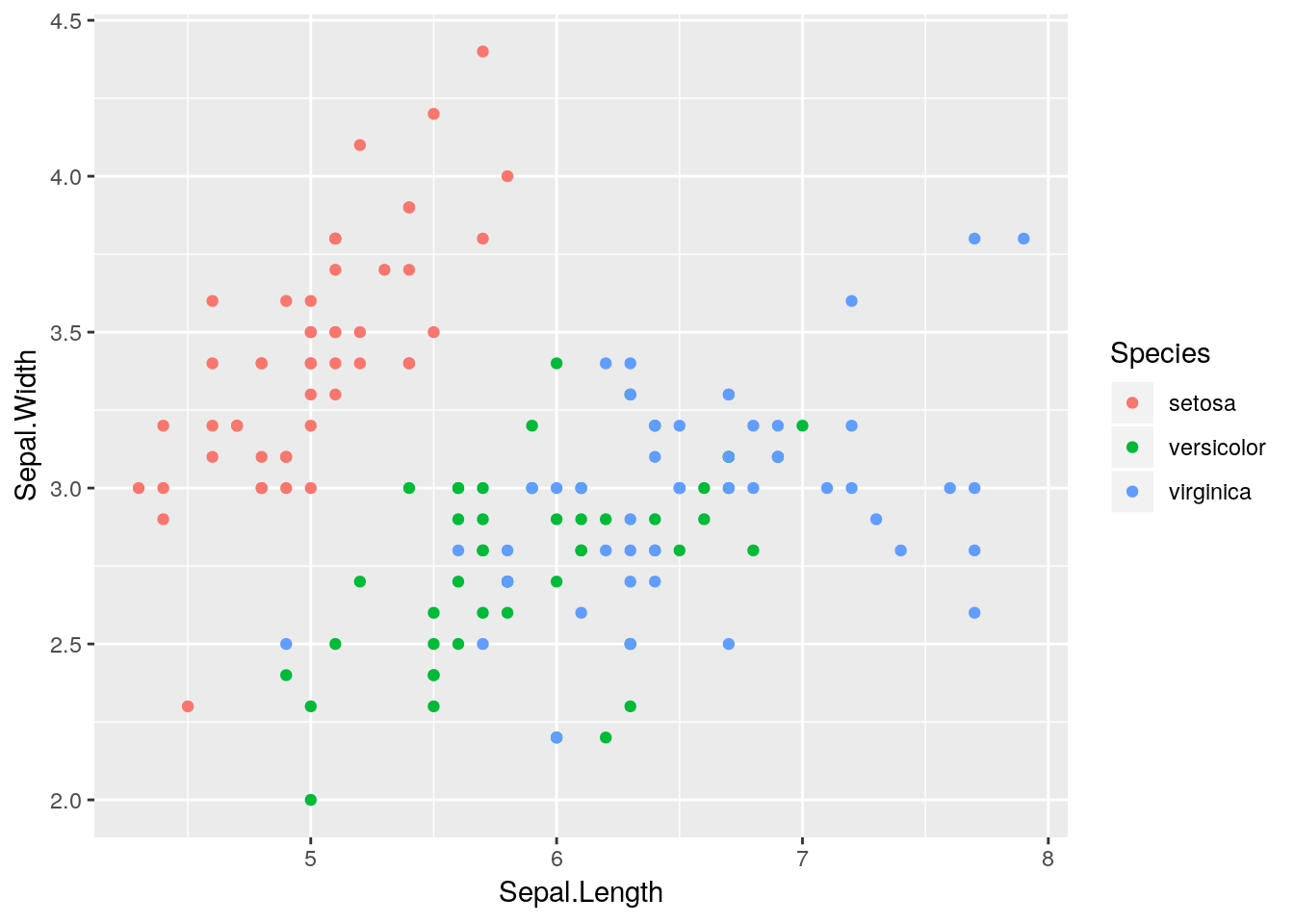

Nice! With one tiny function we have added colours and legends. All nicely formatted to work together in one plot!

Important: Each type of geom accepts only a subset of all aesthetics. Information on these can be found in the help files for each geom_* type, or see also the Data Visualisation Cheat Sheet. Most of these are fairly obvious. For example, a scatterplot requires both x and y aesthetics as a minimum. A kernel density geom e.g. geom_density(), requires only an x aesthetic (we will come back to this shortly). Some aesthetics do not make sense for certain types of geom; for example, it makes sense that a shape aesthetic can be added to geom_point() but not to geom_line(). Conversely, adding a linetype aesthetic to geom_line() makes sense, but not to geom_point().

1.3.3 Labels and titles

Labels and titles can be added fairly easily, using the xlab(), ylab() and ggtitle() functions:

ggplot(iris) +
    geom_point(aes(x = Sepal.Length, y = Sepal.Width, colour = Species)) + 
    xlab("Sepal Length (cm)") + ylab("Sepal Width (cm)") +
    ggtitle("Scatterplot of sepal lengths and widths")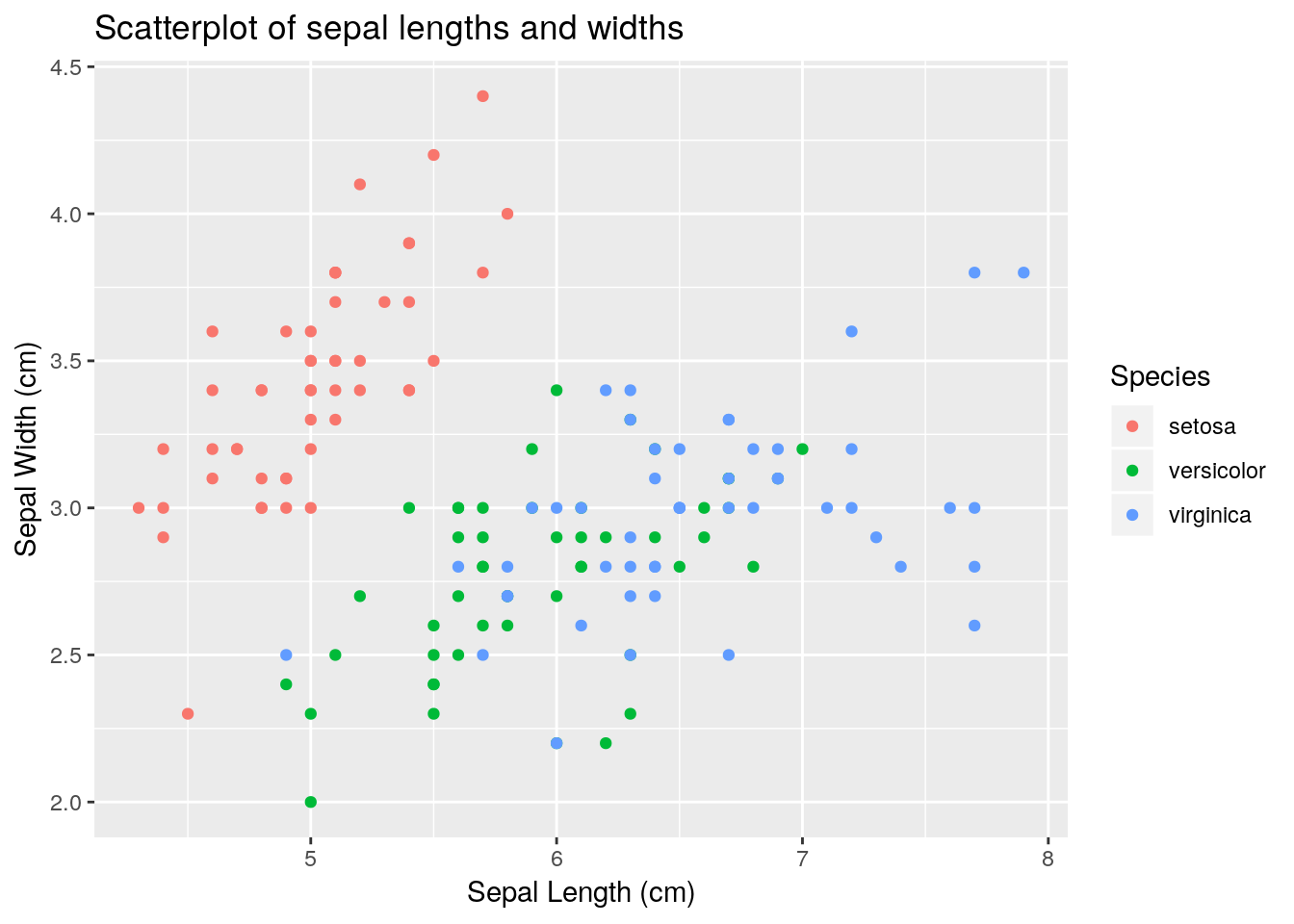

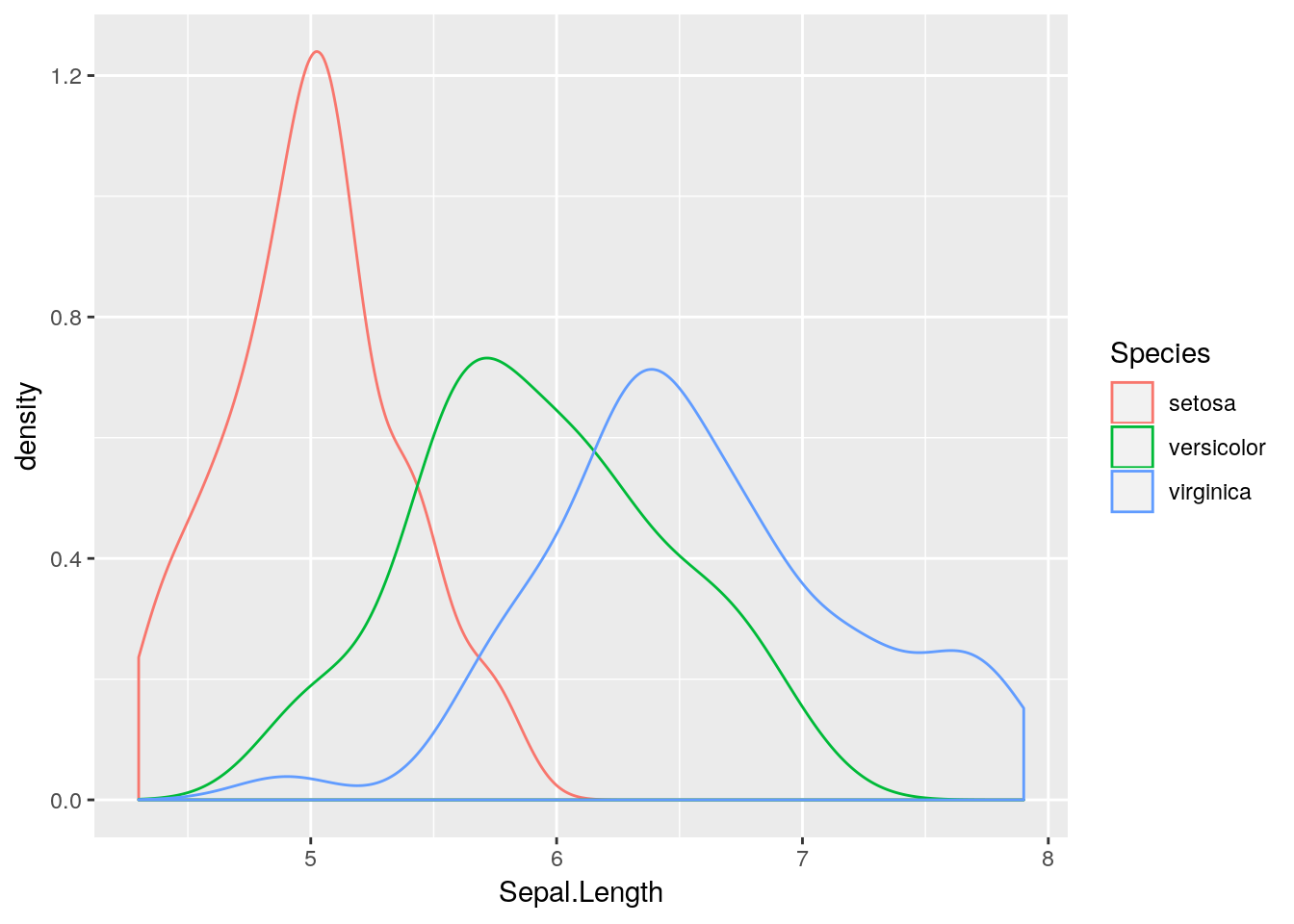
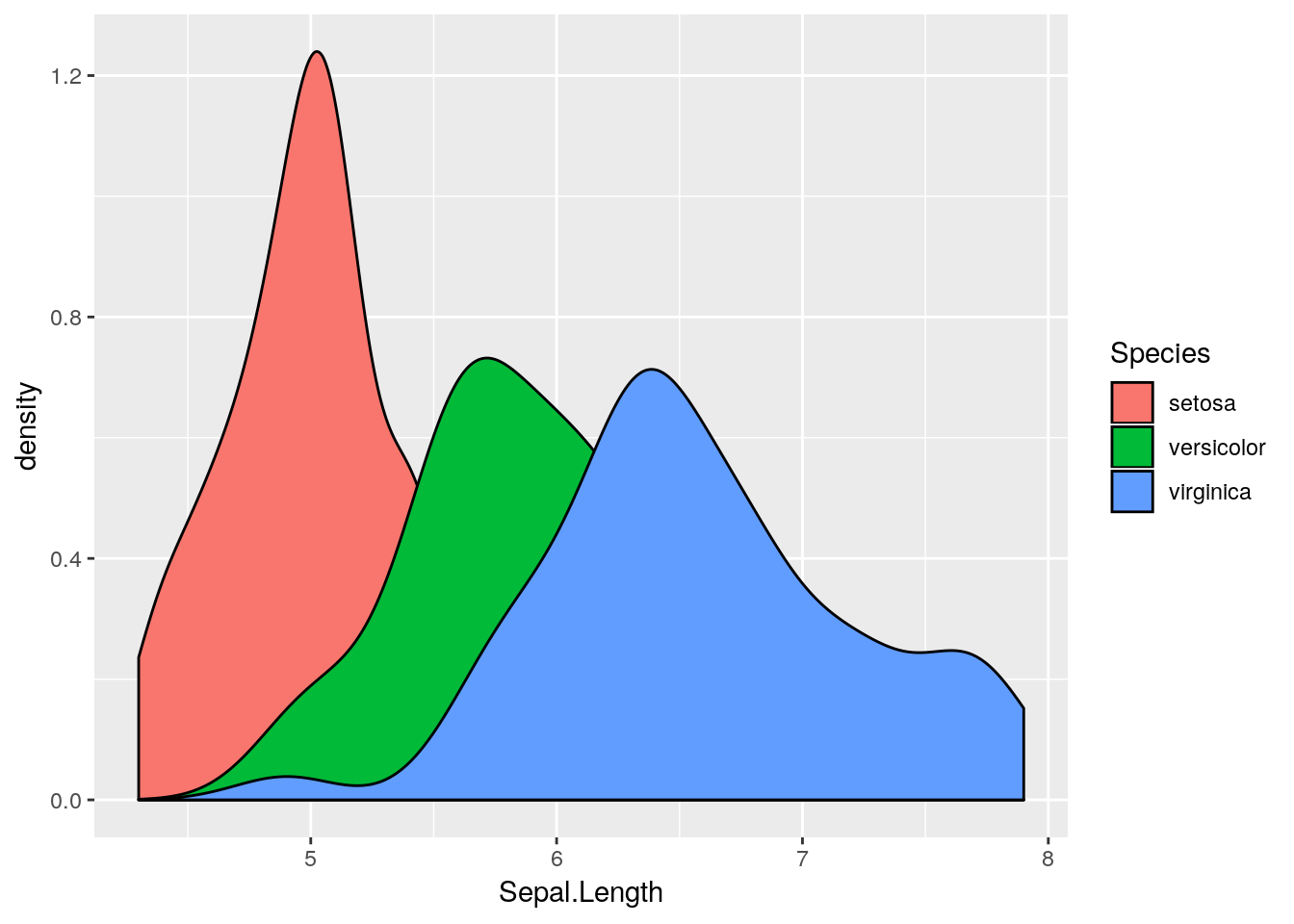
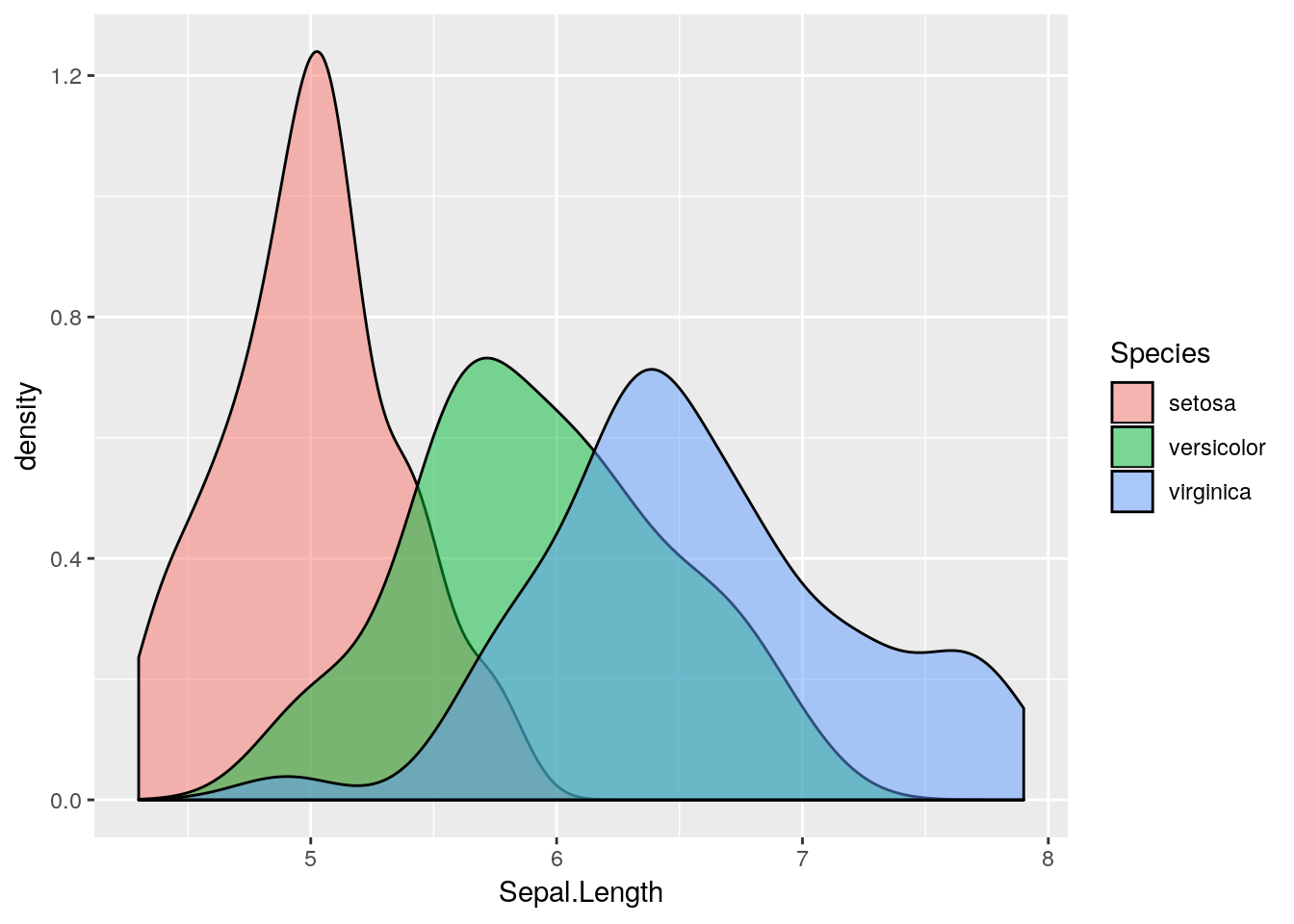
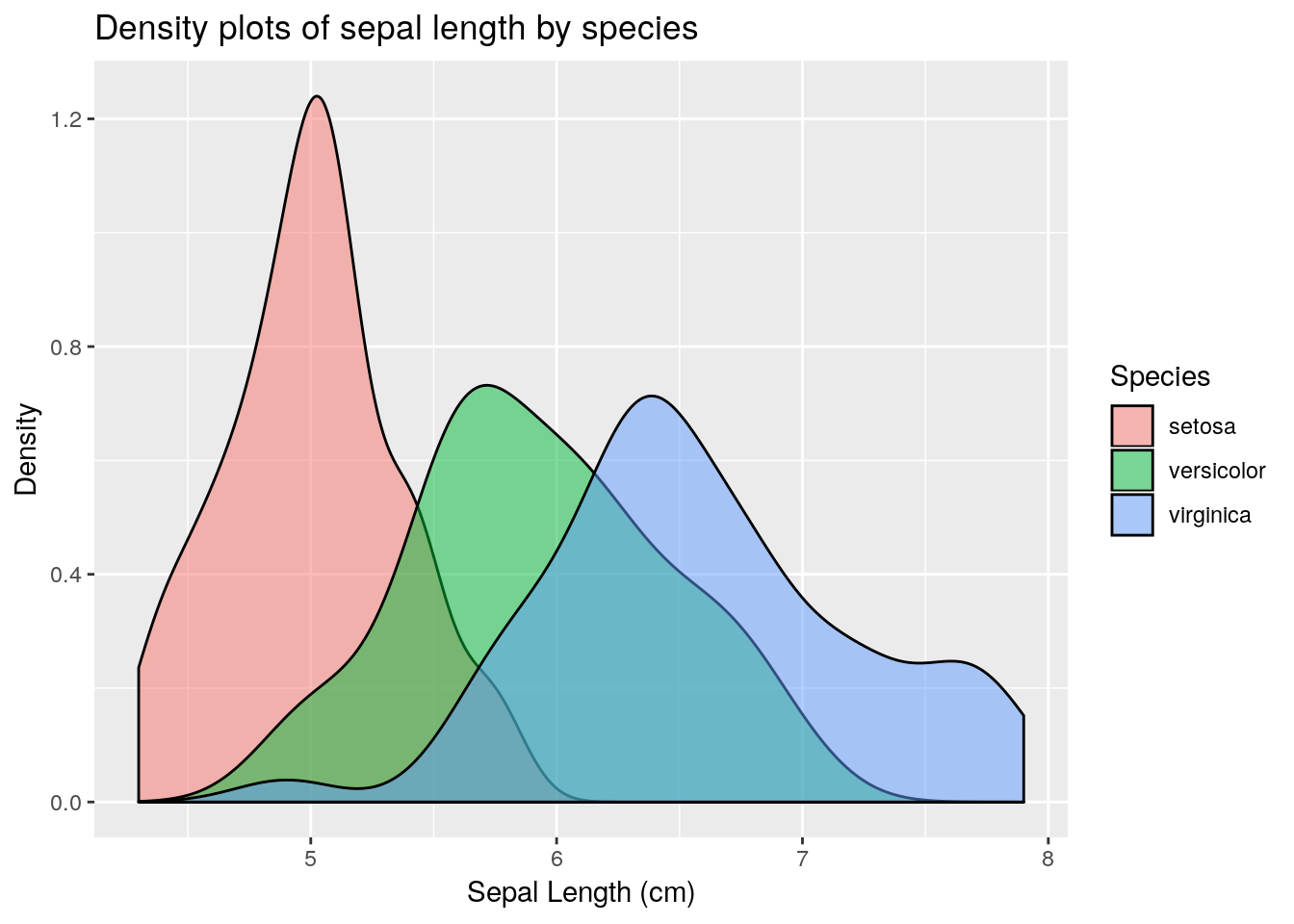
Task

Let’s return to the density plot example. Produce a plot containing three density plots for Sepal.Length, stratified by Species. Hint: use the geom_density() geom, which requires an x aesthetic only.

Solution

ggplot(iris) +
    geom_density(aes(x = Sepal.Length, colour = Species))

Task

Produce the same density plot, but replace the colour aesthetic with a fill aesthetic. What happens?

Solution

ggplot(iris) +
    geom_density(aes(x = Sepal.Length, fill = Species))

We can see that now we have produced filled density plots. However, since these overlap each other, it is difficult to see the full shapes of these distributions.

Task

Now add an alpha channel to this plot. An alpha channel controls the degree of opacity for the colours, where alpha = 0 corresponds to complete transparency, and alpha = 1 to complete opacity. Note that we do not want to map the alpha channel to an aesthetic here, rather we want all fill colours to be, say 50% transparent. We can therefore add an alpha = 0.5 argument to the geom_density() function. What happens?

Solution

ggplot(iris) +
    geom_density(aes(x = Sepal.Length, fill = Species), alpha = 0.5)

Now we can better see the shapes of these distributions.

Task

Tidy up the labels and add a plot title to produce a final plot.

Solution

ggplot(iris) +
    geom_density(aes(x = Sepal.Length, fill = Species), alpha = 0.5) + 
    xlab("Sepal Length (cm)") + ylab("Density") + 
    ggtitle("Density plots of sepal length by species")

1.3.4 Aside: aesthetics vs. generic options

As a quick aside, notice that when we set the alpha channel above, we did not set it as an aesthetic, rather we set it as a generic option which was applied to all components of the plot. Perhaps the easiest way to visualise this difference, is to consider different colour options. Take a look at these next pieces of code and try to understand the differences between them.

ggplot(iris) +
    geom_point(aes(x = Sepal.Length, y = Sepal.Width, colour = Species))

ggplot(iris) +
    geom_point(aes(x = Sepal.Length, y = Sepal.Width), colour = "red")

Task

What happens if you try to run the following code?

ggplot(iris) +
    geom_point(aes(x = Sepal.Length, y = Sepal.Width), colour = Species)

Why does this happen?

Solution

In this case you get an error:

ggplot(iris) +
    geom_point(aes(x = Sepal.Length, y = Sepal.Width), colour = Species)

## Error in layer(data = data, mapping = mapping, stat = stat, geom = GeomPoint, : object 'Species' not found

This is because you are trying to set a generic colour using a vector object Species. Since the colour option is not part of the aesthetics, ggplot() does not know where to find Species.

1.3.5 Faceting

Another really useful feature of ggplot is the ability to use faceting to display sub-plots according to some grouping variable. For example, let’s assume that we want to produce separate plots of sepal length vs. width for each of the three species of iris. We can do this using faceting:

ggplot(iris) +
    geom_point(aes(x = Sepal.Length, y = Sepal.Width)) +
    facet_wrap(~ Species)

Neat eh? Note that we can also use different aesthetics within the facets. For example, we could also add a colour aesthetic e.g.

ggplot(iris) +
    geom_point(aes(x = Sepal.Length, y = Sepal.Width, colour = Species)) +
    facet_wrap(~ Species)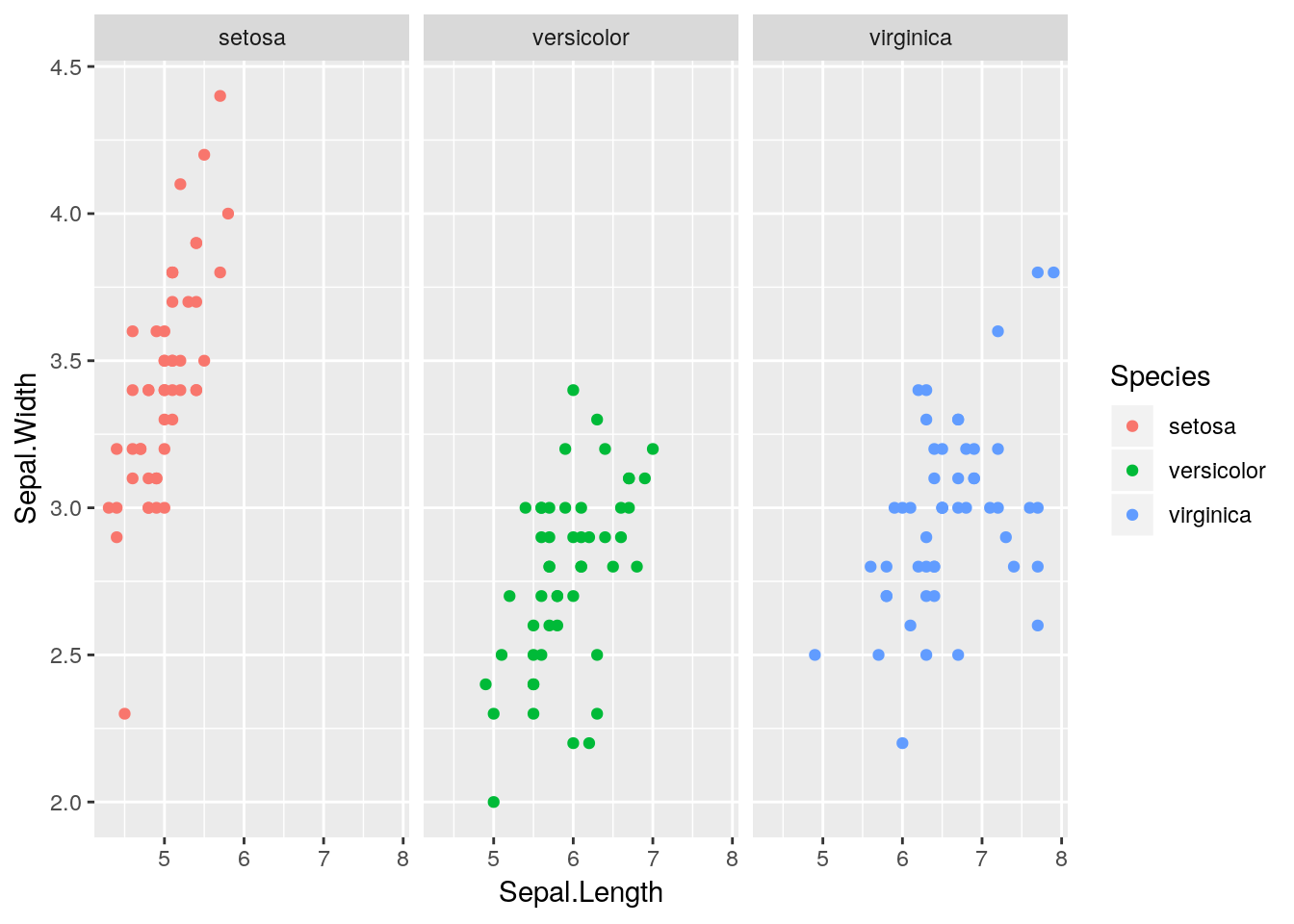

This doesn’t add anything more to the plot here since the colours are redundant. Later we will see a better example of this.

Note there is also a facet_grid() option that allows us to facet by more than one variable. Please see the Data Visualisation Cheat Sheet for more details.

1.3.6 Statistical transformations

Another feature of ggplot2 is that we can layer transformations over the top of our raw data. For example, there is a stat_smooth() function that allows us to overlay a smoothed non-parametric line to a scatterplot. For example:

ggplot(iris) +
    geom_point(aes(x = Sepal.Length, y = Sepal.Width)) +
    stat_smooth(aes(x = Sepal.Length, y = Sepal.Width))

## `geom_smooth()` using method = 'loess' and formula 'y ~ x'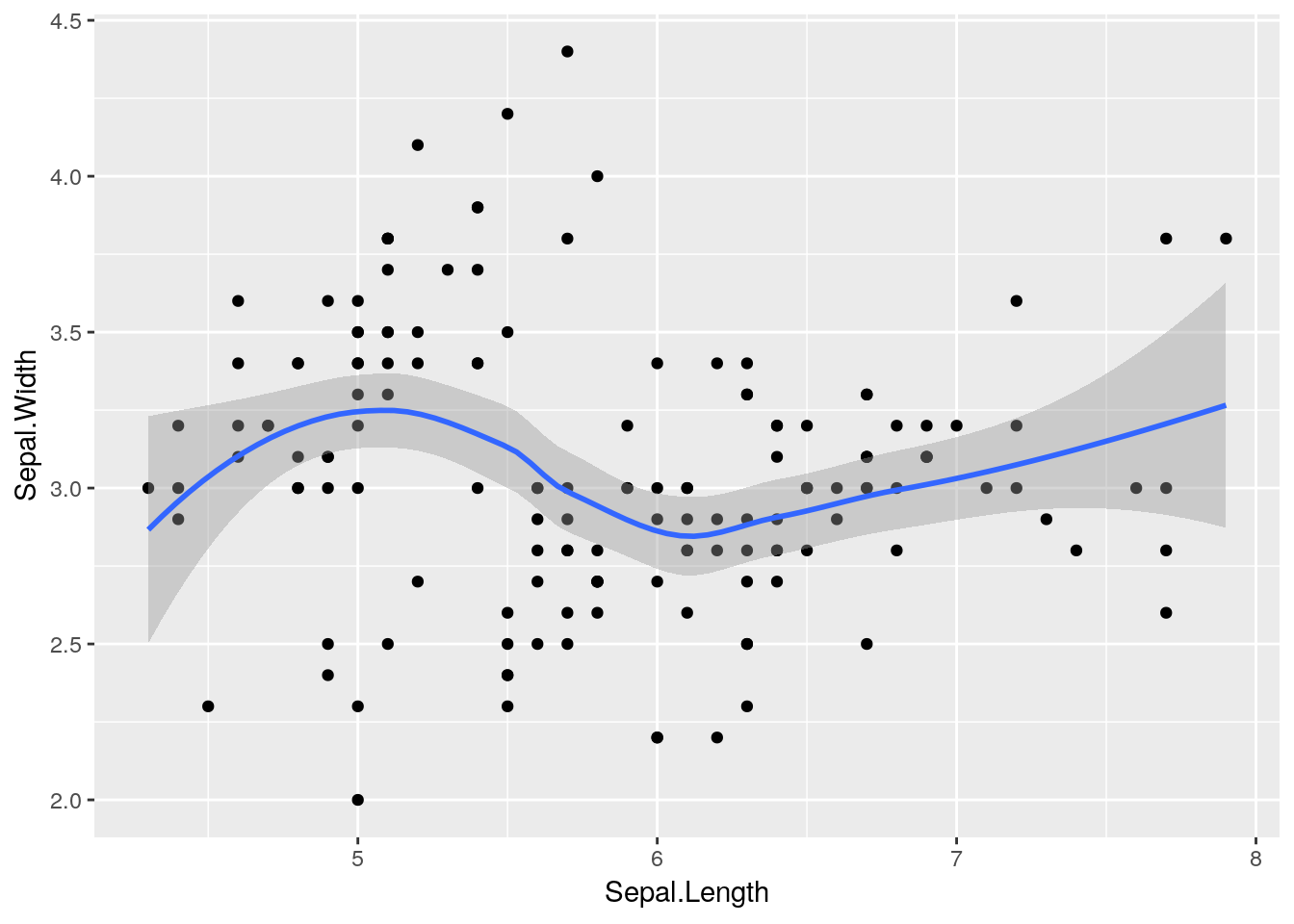

Notice that this has added a loess smoothed line to the plot². We could instead add a linear line if we prefer, by setting a method argument to stat_smooth e.g.

ggplot(iris) +
    geom_point(aes(x = Sepal.Length, y = Sepal.Width)) +
    stat_smooth(aes(x = Sepal.Length, y = Sepal.Width), method = "lm")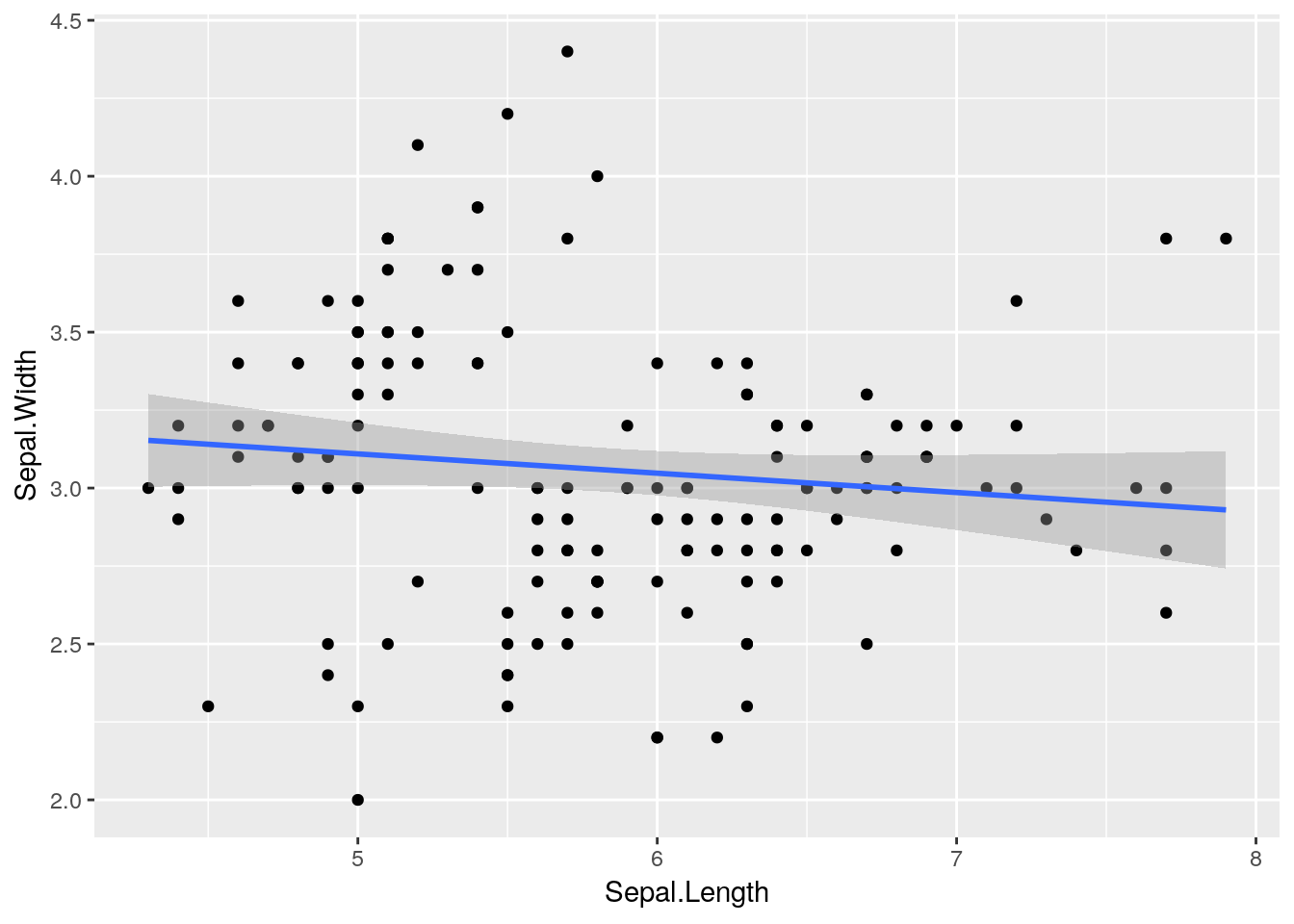

With the addition of a single function we can now add different lines for each species:

ggplot(iris) +
    geom_point(aes(x = Sepal.Length, y = Sepal.Width)) +
    stat_smooth(aes(x = Sepal.Length, y = Sepal.Width), method = "lm") +
    facet_wrap(~ Species)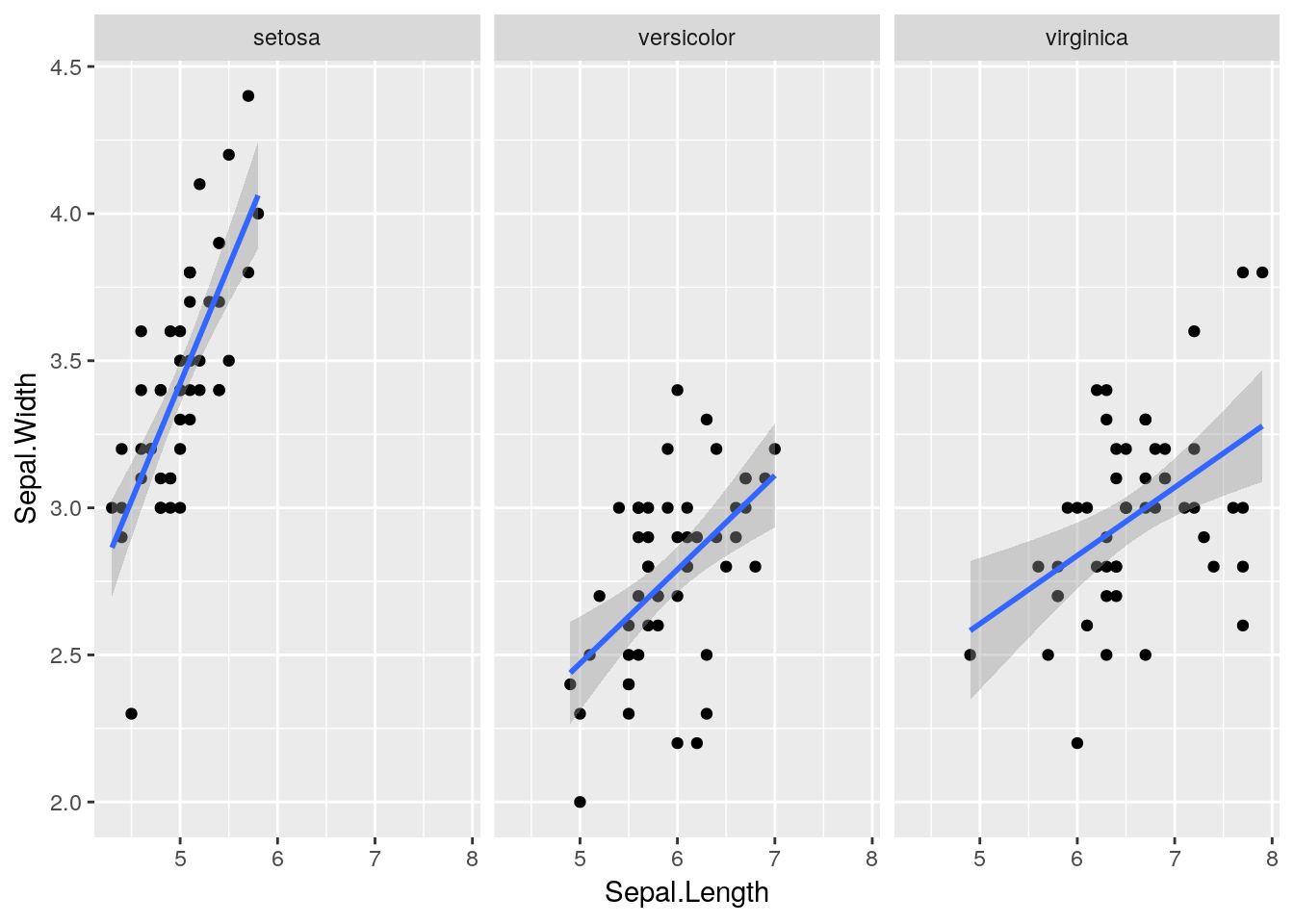

Aside: this is a neat example of Simpson’s Paradox, which an apparent trend in the data disappears or reverses when the trend is explored in subsets of the data. (In this case the linear model suggested a negative correlation between sepal length and width when the species information was ignored, but a positive correlation within each species.)

1.3.7 Aside: “global” vs. “local” options

Notice that in the code below the geom_point() and stat_smooth() functions use the same aesthetics. In this case it is possible to add “global” aesthetics to a plot through the ggplot2() function, which can then be accessed by sub-functions. Hence the following two pieces of code are equivalent here.

ggplot(iris) +
    geom_point(aes(x = Sepal.Length, y = Sepal.Width)) +
    stat_smooth(aes(x = Sepal.Length, y = Sepal.Width), method = "lm") +
    facet_wrap(~ Species)

ggplot(iris, aes(x = Sepal.Length, y = Sepal.Width)) +
    geom_point() +
    stat_smooth(method = "lm") +
    facet_wrap(~ Species)

Mixtures of “global” and “local” aesthetics can be used where necessary, which is particularly useful when layering information from different data sets onto the same plot.

1.3.8 Scales

Scales control the details of how data values are translated to visual properties. These allow us to control translations from data to aesthetics. We will see some simple examples of these in due course.

1.4 A more complex example: Gapminder

Let’s take these ideas and return to our Gapminder data. Datasets from the Gapminder project can be downloaded from https://www.gapminder.org/data. However, the particular data set required to replicate Figure 1.1 is available in a package in R called (naturally) gapminder. If not already installed, then this can be installed in the usual way e.g.

install.packages("gapminder")

Once you have it installed we need to load the packages.

library(gapminder)

To have a quick look at the data, which are available as an object called gapminder.

gapminder

## # A tibble: 1,704 x 6
##    country     continent  year lifeExp      pop gdpPercap
##    <fct>       <fct>     <int>   <dbl>    <int>     <dbl>
##  1 Afghanistan Asia       1952    28.8  8425333      779.
##  2 Afghanistan Asia       1957    30.3  9240934      821.
##  3 Afghanistan Asia       1962    32.0 10267083      853.
##  4 Afghanistan Asia       1967    34.0 11537966      836.
##  5 Afghanistan Asia       1972    36.1 13079460      740.
##  6 Afghanistan Asia       1977    38.4 14880372      786.
##  7 Afghanistan Asia       1982    39.9 12881816      978.
##  8 Afghanistan Asia       1987    40.8 13867957      852.
##  9 Afghanistan Asia       1992    41.7 16317921      649.
## 10 Afghanistan Asia       1997    41.8 22227415      635.
## # … with 1,694 more rows

Here we can see that the data set consists of 1704 rows and 6 columns, and contains information on country, continent, life expectancy, population size, GDP (per capita) and year.

The R aficionados amongst you might notice the slightly strange print behaviour of the gapminder object. If we try to print a data.frame object to the screen, then it usually prints the whole object. Here it’s printed an attenuated version of the object. This is because the gapminder data set is saved as a tibble object, rather than a standard data.frame.

Aside: A tibble is an enhanced data.frame object which are generally easier to examine. For example, they force R to display only the data that fits onscreen. It also adds some information about the class of each column. In fact, the tibble package—loaded as part of the tidyverse—introduces the as_tibble() function to convert ordinary data.frame objects to tibble objects, in case you want to use this functionality in future. Please see the Data Import Cheat Sheet for more information.

Note also that tibble objects seem to make a distinction between integers (<int>) and doubles (<dbl>), instead of just using numeric. R makes no such distinction in practice, and so you can think of either of these as simply numeric types.

We’ll use tibbles more generally in the later data wrangling session.

Let’s just clarify the data:

• country: country of interest (factor);
• continent: continent country can be found in (factor);
• year: year corresponding to data (in increments of 5 years) (numeric);
• lifeExp: life expectancy at birth (in years) (numeric);
• pop: population size (numeric);
• gdpPercap: GDP per capita, in dollars, by Purchasing Power Parities and adjusted for inflation (numeric).

1.4.1 GDP against life expectancy

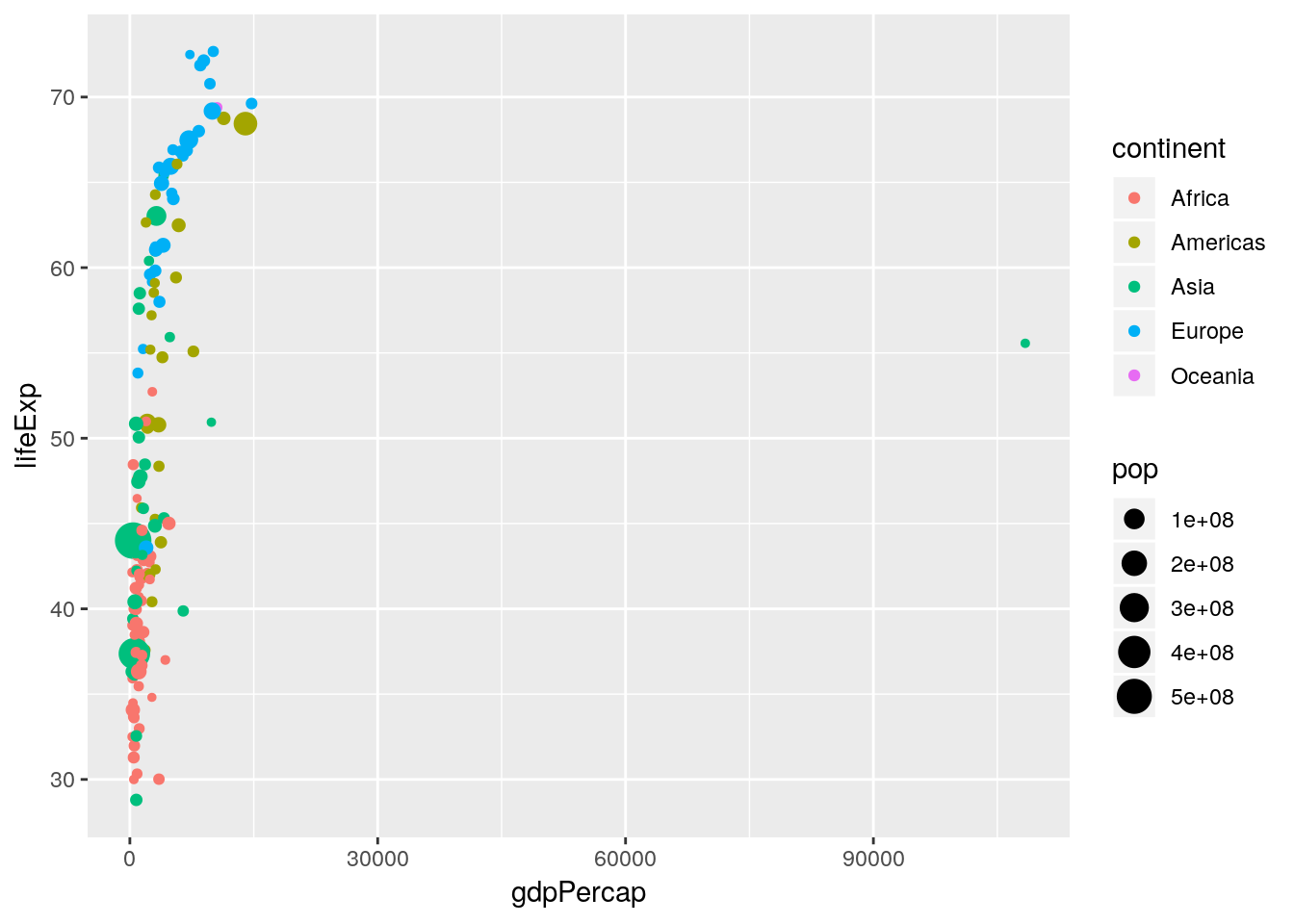
Let’s think about Figure 1.1 and try to map the various aesthetics in the plot to our data set. We have:

Table 1.1: Aesthetics for gapminder plot

Aesthetic	Variable
x	gdpPercap
y	lifeExp
colour	continent
size	pop

Task

Using ggplot2, produce a scatterplot that uses the aesthetics in Table 1.1 for just the year 1952.

Solution

ggplot(gapminder[gapminder$year == 1952, ], 
       aes(x = gdpPercap, y = lifeExp, size = pop, colour = continent)) +
    geom_point() 

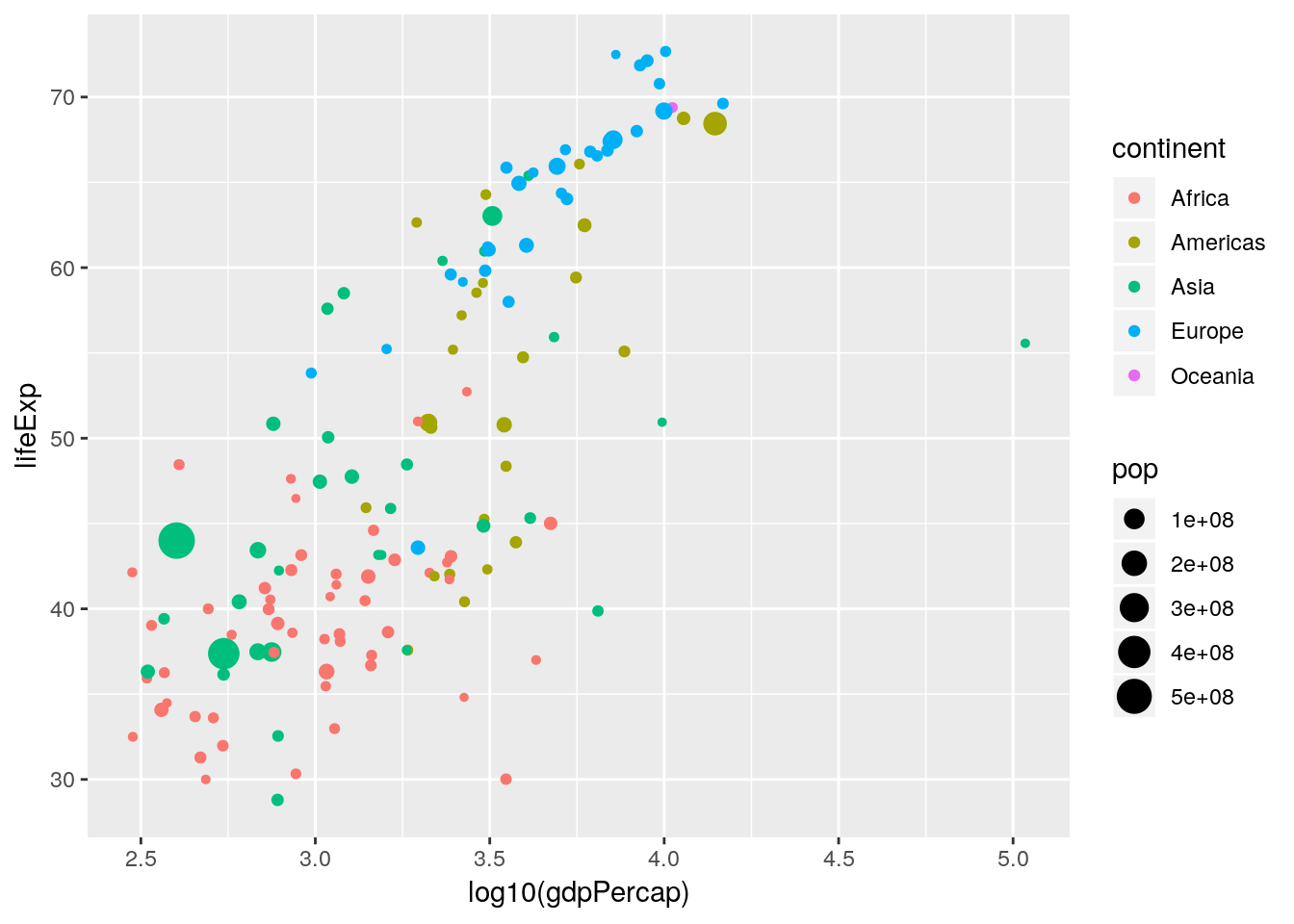
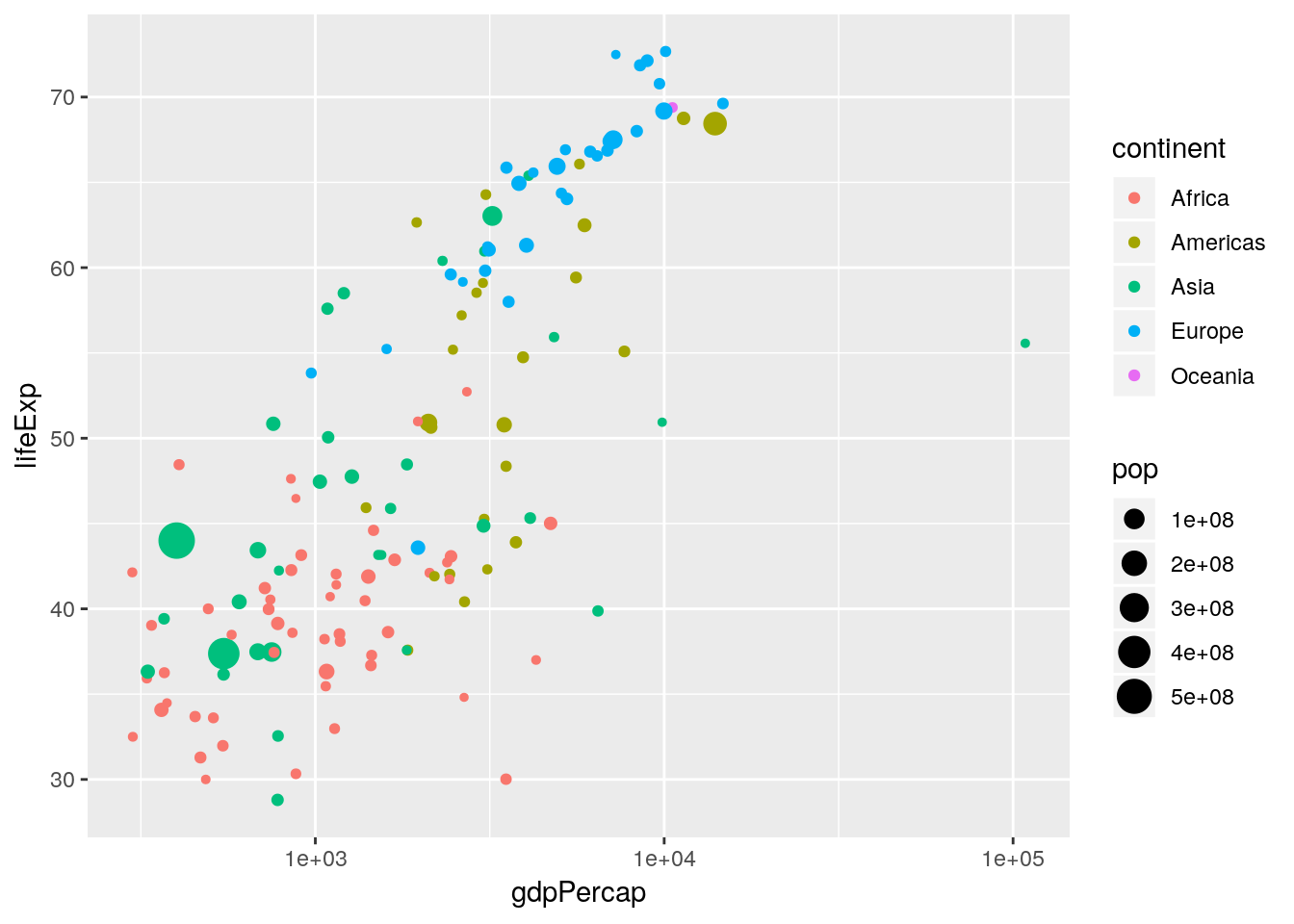
Notice how rich this plot is already. One thing to note is that in Figure 1.1 the \(x\)-axis is plotted on the \(\log_{10}\) scale. There are two ways in which we can handle this: either by transforming the gdpPercap variable directly, or by using an appropriate scales_* function. Here we want to apply a \(\log_{10}\) transformation to the x aesthetic.

Task

1. Redo the previous plot but with the aesthetic x = log10(gdpPercap).
2. Redo the previous plot with the aesthetic x = gdpPercap but with an additional scale_x_log10() layer.

How do these plots differ?

Solution

ggplot(gapminder[gapminder$year == 1952, ], 
       aes(x = log10(gdpPercap), y = lifeExp, size = pop, colour = continent)) +
    geom_point() 

ggplot(gapminder[gapminder$year == 1952, ], 
       aes(x = gdpPercap, y = lifeExp, size = pop, colour = continent)) +
    geom_point() + scale_x_log10()

The plots differ purely in the labels for the \(x\)-axis.

Important: ggplot2 also allows you to save the plot as an object, which can be updated at a later date or used within other functions. For example,

p <- ggplot(gapminder[gapminder$year == 1952, ], 
      aes(x = gdpPercap, y = lifeExp, size = pop, colour = continent)) +
   geom_point()

creates an object called p that contains the plot information. This will not be plotted until the object is printed to the screen e.g.

p

Note: If using ggplot inside functions you may have to explicitly use the print() function (e.g. print(p)).

This can be useful if we want to add things to an existing plot at a later stage without having to rewrite the entire plot. For example, to set the scales on plot p we can do:

p <- p + scale_x_log10()
p

ggplot2 has lots of built in transformations e.g. "log", "exp", "sqrt", "log10" and so on. Or you can define your own. Notice that we have not transformed the data, we have merely told ggplot() on what scale to plot it. This sorts out the axis tick labelling automatically.

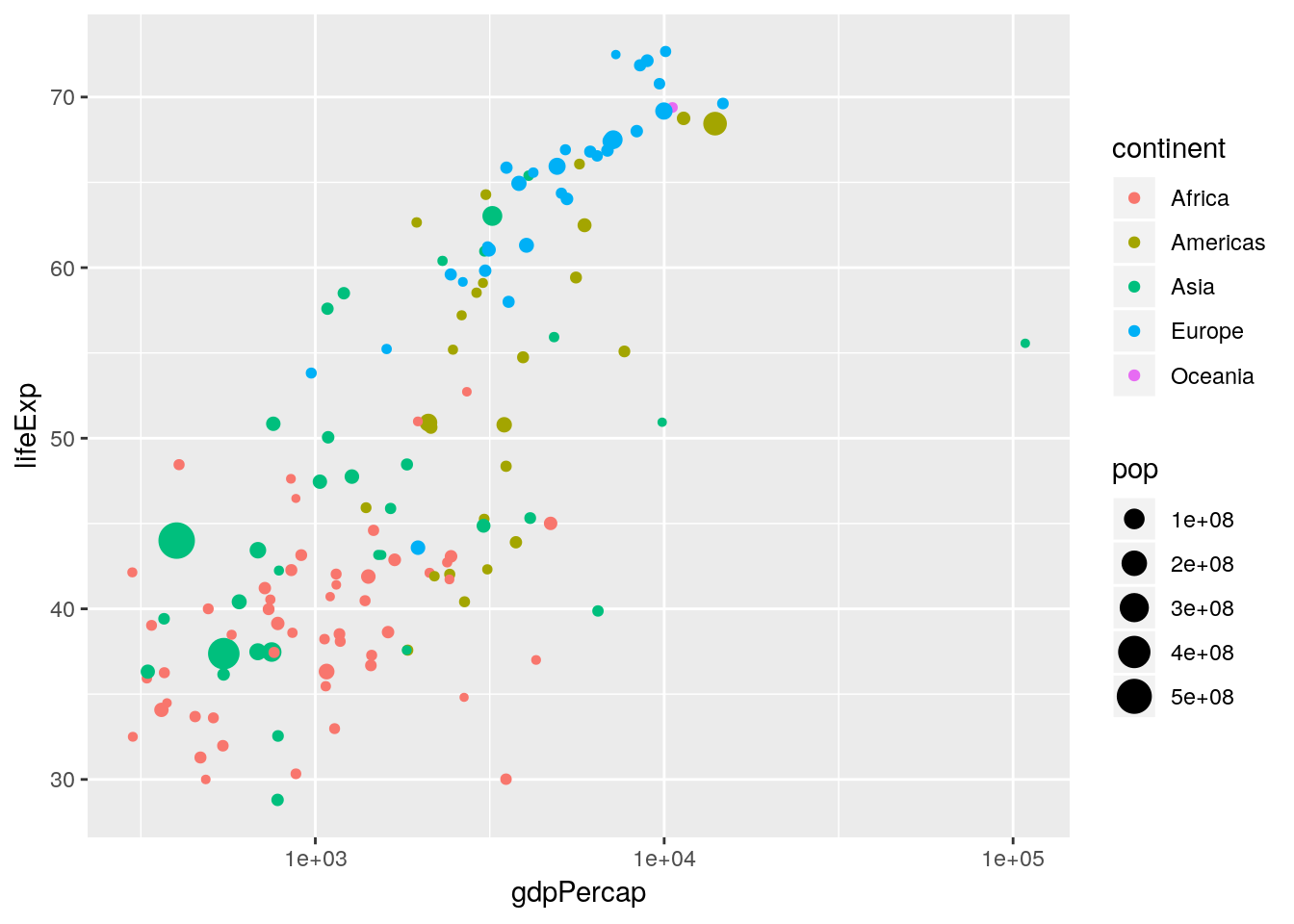
We can also scale other aesthetics. For example, although the relative areas of the points are scaled nicely, we probably want the largest points to be slightly larger. Hence we can scale the area of the maximum point by using the scale_size_area() function:

p <- p + scale_size_area(max_size = 10)
p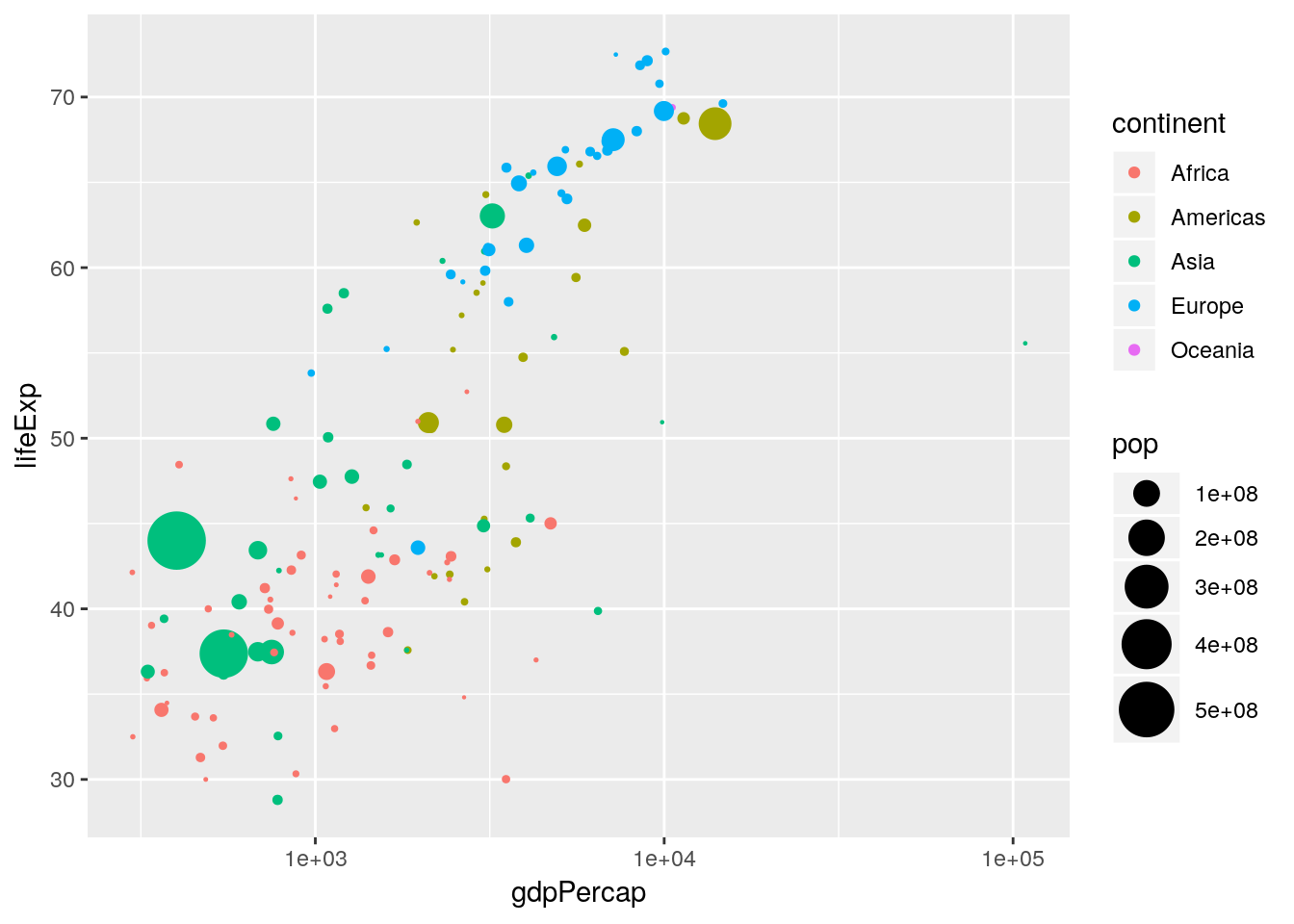

Again, labels and titles can be added fairly easily, using the xlab(), ylab() and ggtitle() functions:

p <- p + xlab("log10(GDP per capita)") +
    ylab("Life expectancy at birth (years)") +
    ggtitle("1952")
p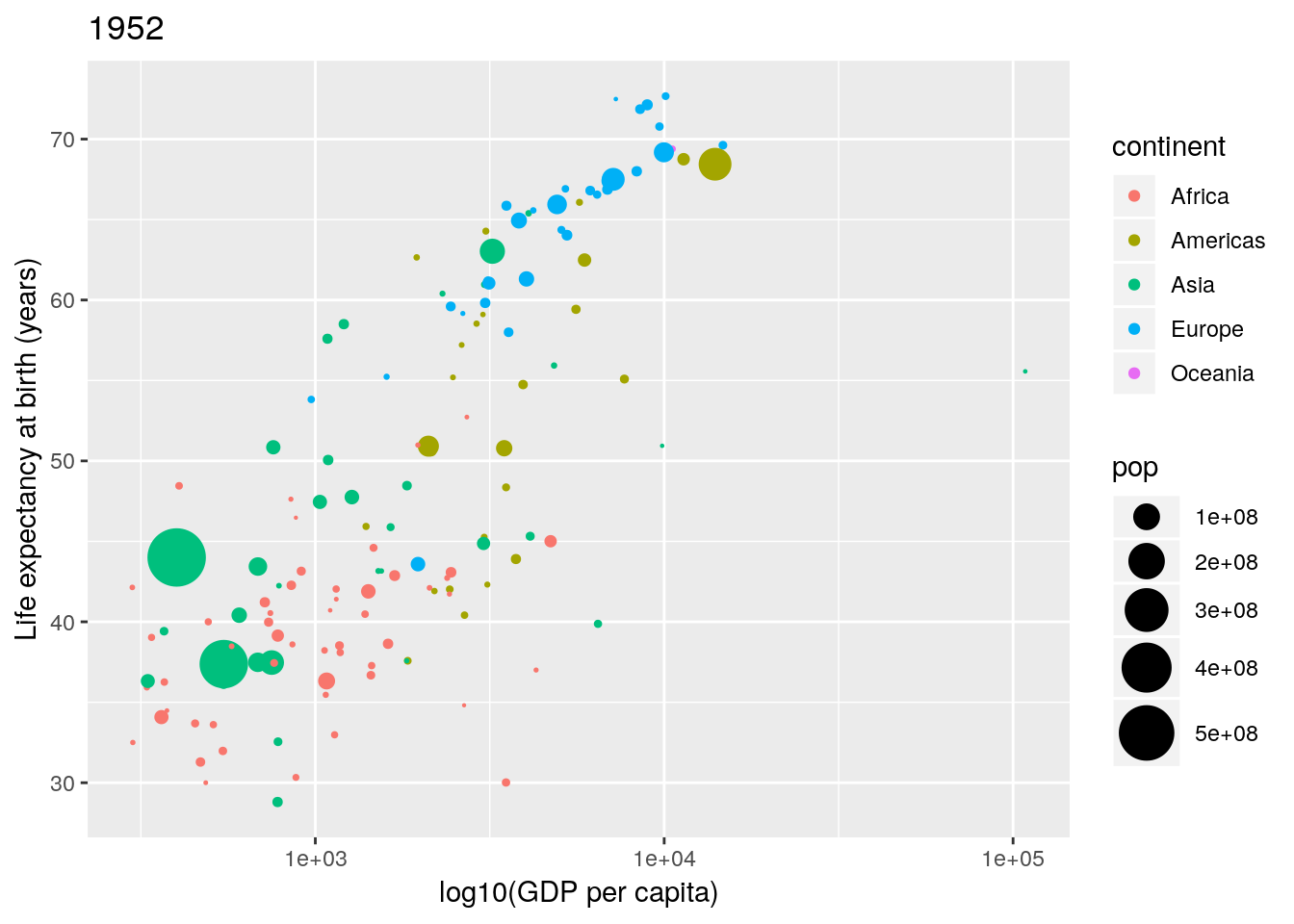

Changing the legend titles can also be done using the labs() option. Notice that the legends map to the aesthetics, so there is a colour legend that maps to the colour aesthetic, and a size legend that maps to the size aesthetic.)

p <- p + labs(colour = "Continent", size = "Population size")
p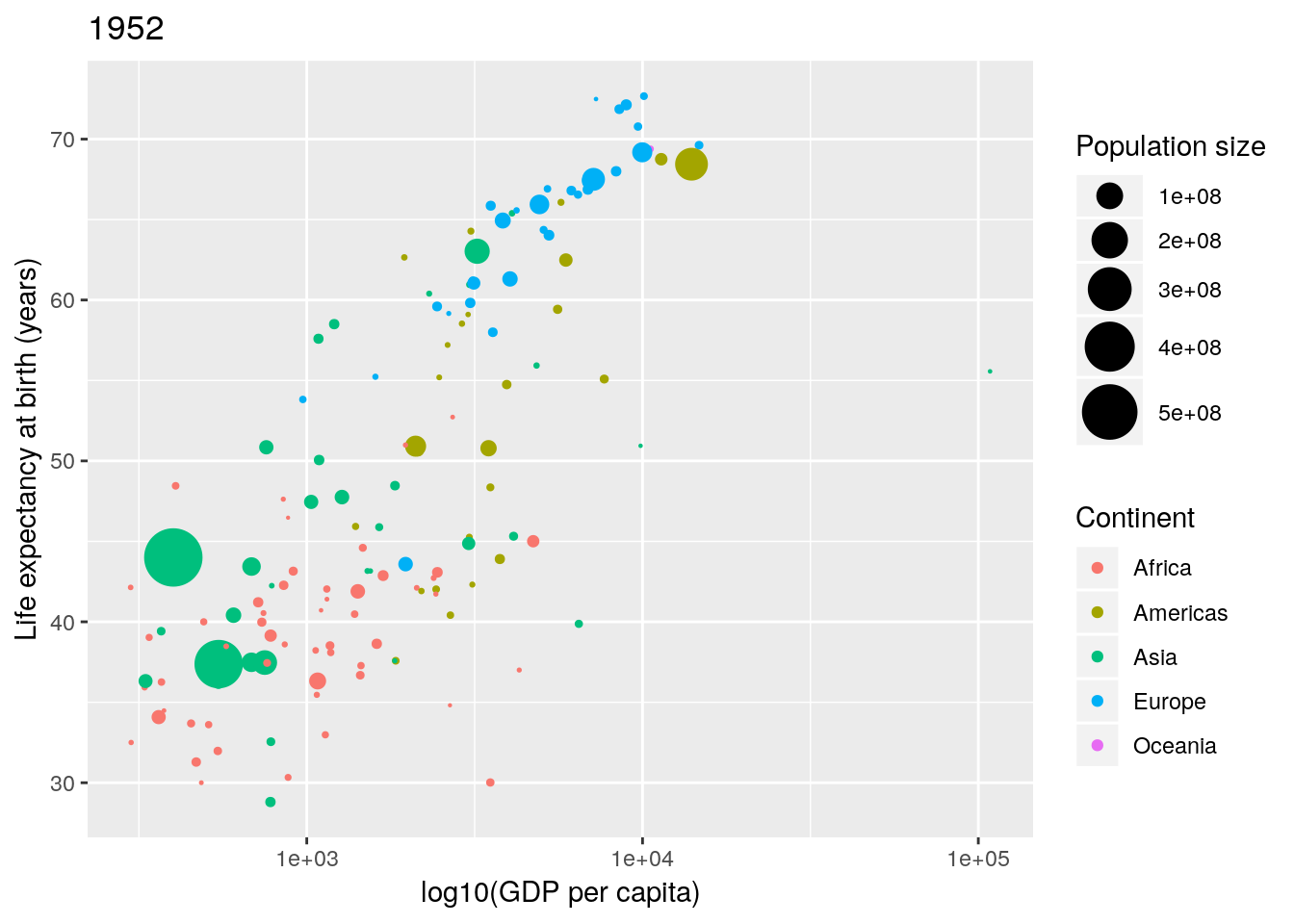

Not bad. Finally notice that by default ggplot2 uses a light-grey background. This seems to prove somewhat divisive. There is a solid theory behind choosing this as the default, since it provides clarity without having too much contrast. However, some people don’t like it, and so there are options to turn this off (using theme()). In this case we can simply turn this off using theme_bw() (a black-and-white theme).

p <- p + theme_bw()
p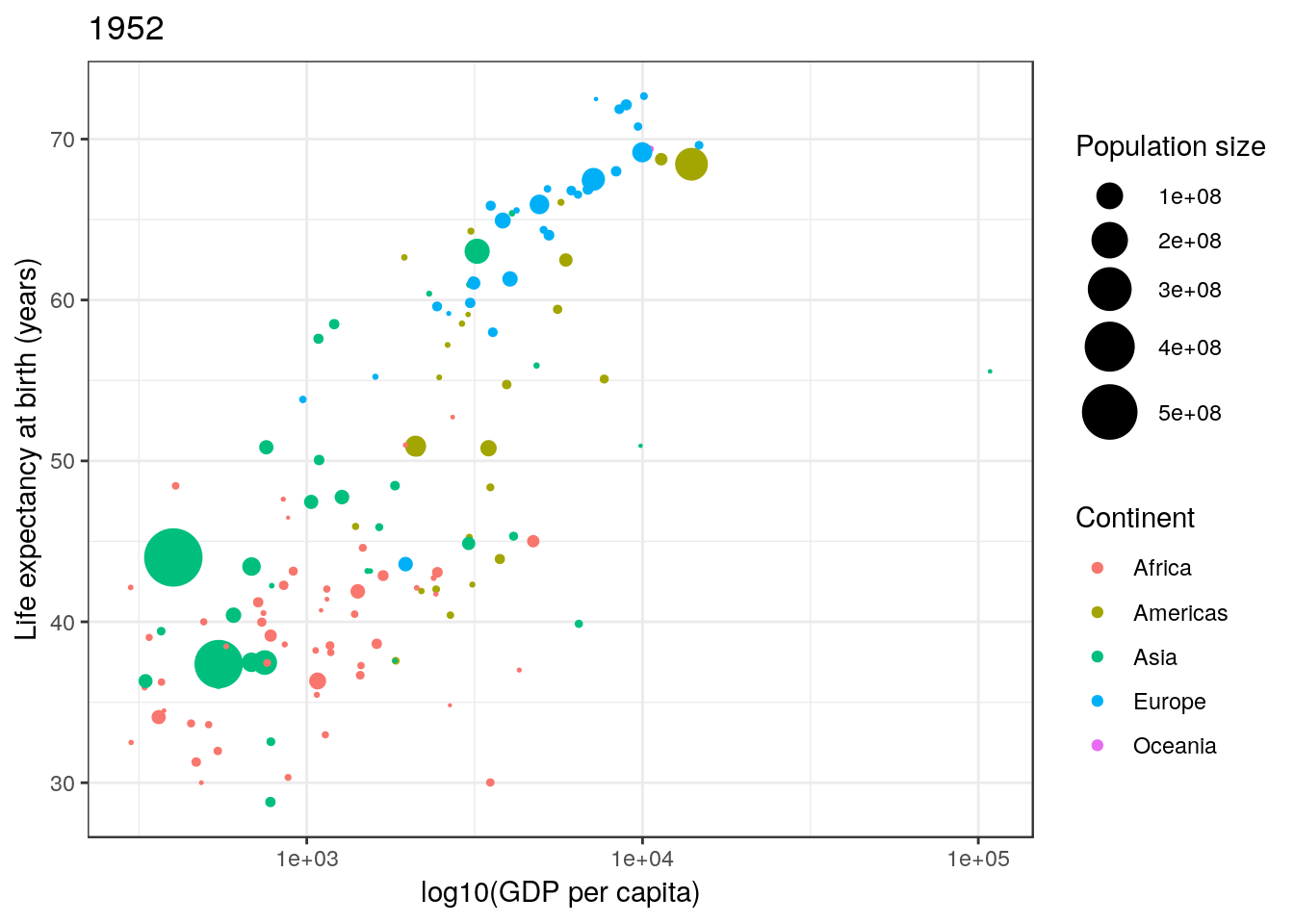

There are many, many possible options with ggplot2. Far too many to cover here. We can only really get a flavour of what can be achieved. I have often found Google to be invaluable for learning ggplot2.

Let’s have a look at a couple of other examples.

1.4.2 GDP per continent

Another chart seen in Professor Rosling’s TED talk was a stacked density plot. This is a smoothed version of a histogram. Let’s start by looking at the distribution of GPD values across all countries in 1952. This can be done with the geom_density() geom as in the earlier example, which requires only an x aesthetic—see ?geom_density—since it calculates the density on the \(y\)-axis automatically from the data once we have chosen an appropriate bandwidth.

ggplot(gapminder[gapminder$year == 1952, ],
       aes(x = gdpPercap)) +
    geom_density() +
    scale_x_log10()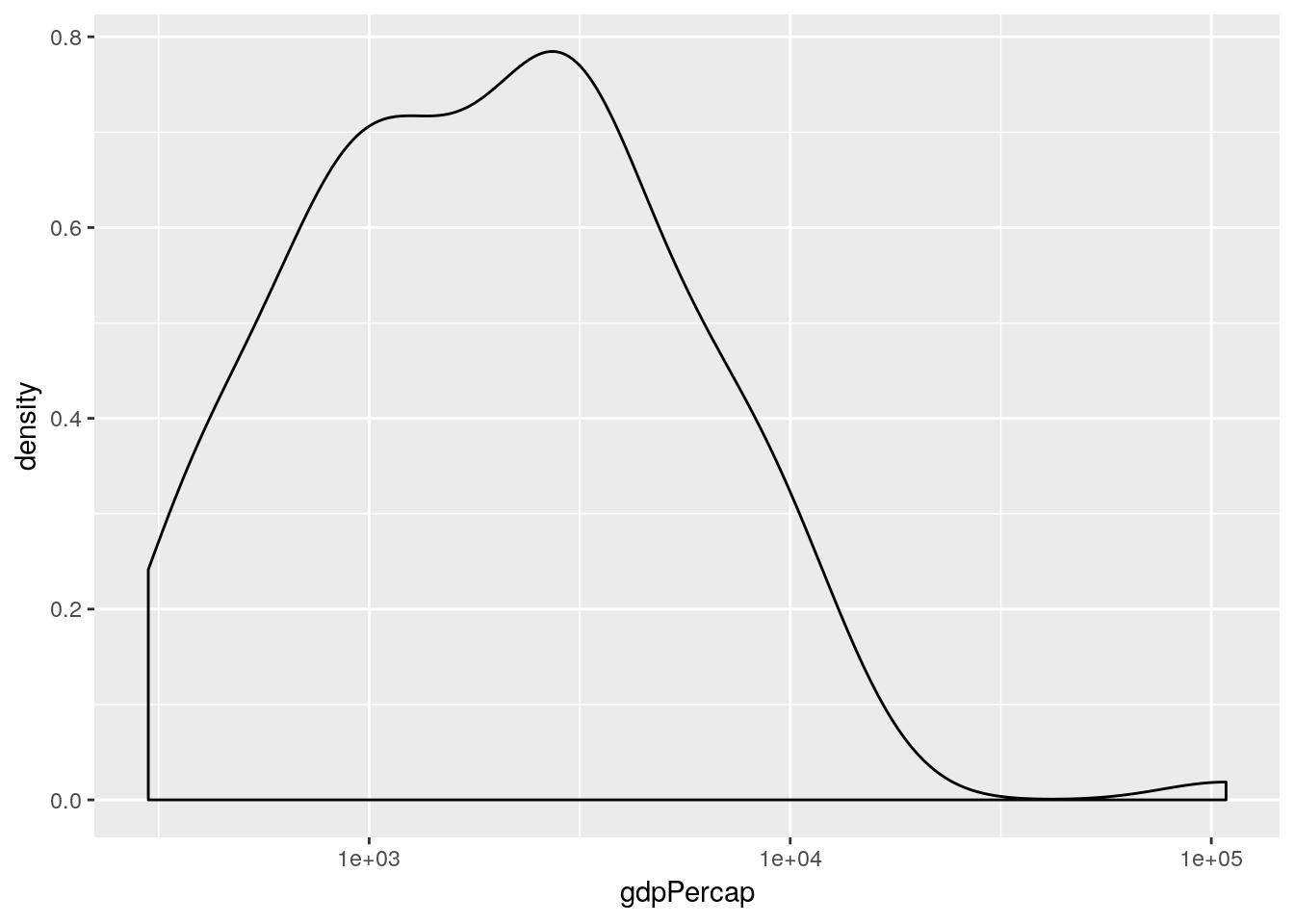

This simple plot is producing a density plot of the distribution of GDP across all countries in 1952. How do split this by continent? Well, there are various ways. One way would be to set the fill aesthetic to map to the continent variable:

ggplot(gapminder[gapminder$year == 1952, ],
       aes(x = gdpPercap, fill = continent)) +
    geom_density() +
    scale_x_log10()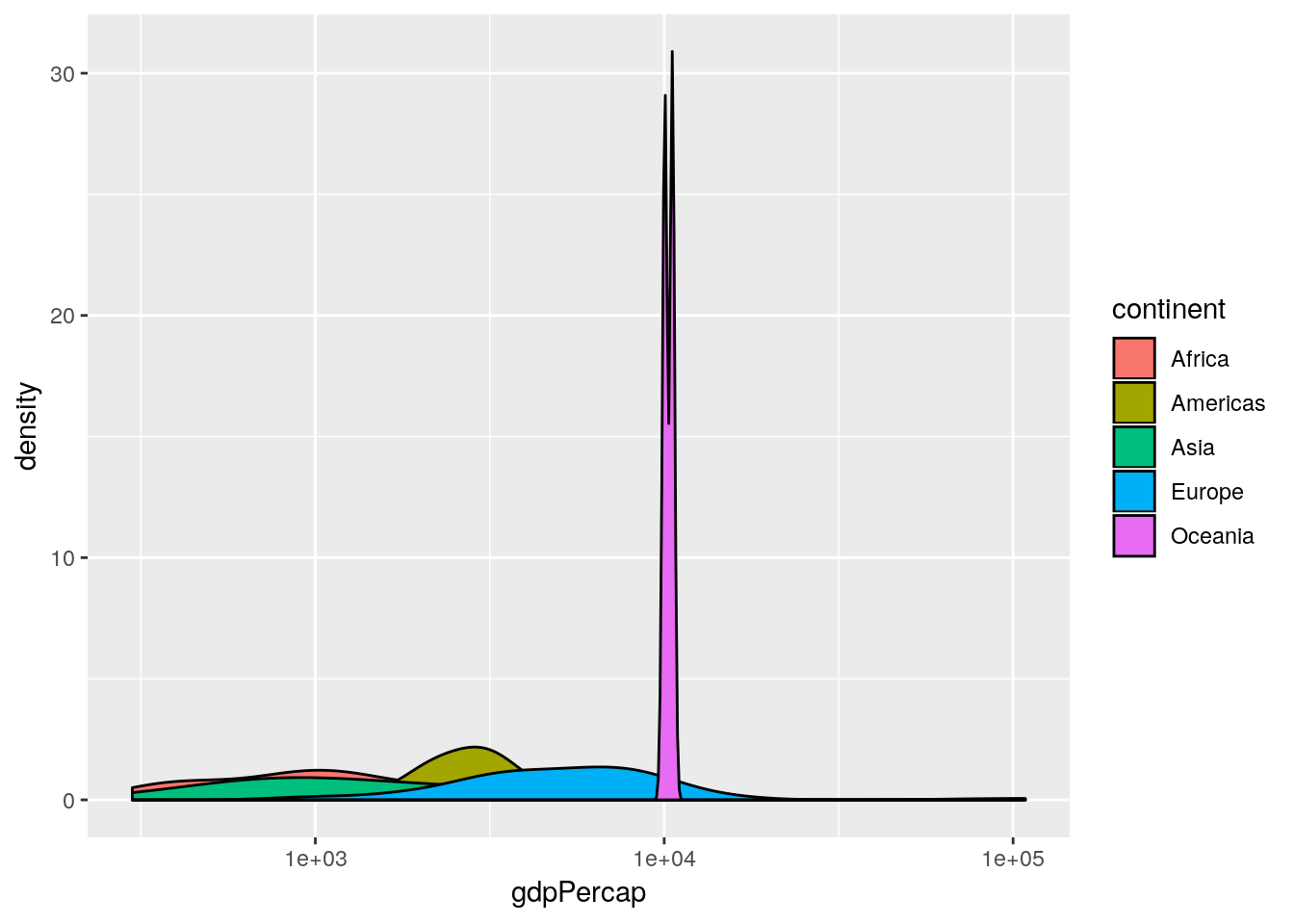

This produces an overlapped density plot by default. (The patterns are quite difficult to see here, due to the Oceania data, so for the purposes of exposition only we’re going to remove Oceania from the subsequent plots.)

## remove Oceania (for exposition purposes only)
gapminderNoOc <- gapminder[gapminder$continent != "Oceania", ]

## produce overlapped density plot
ggplot(gapminderNoOc[gapminderNoOc$year == 1952, ],
       aes(x = gdpPercap, fill = continent)) +
    geom_density(alpha = 0.5) +
    scale_x_log10()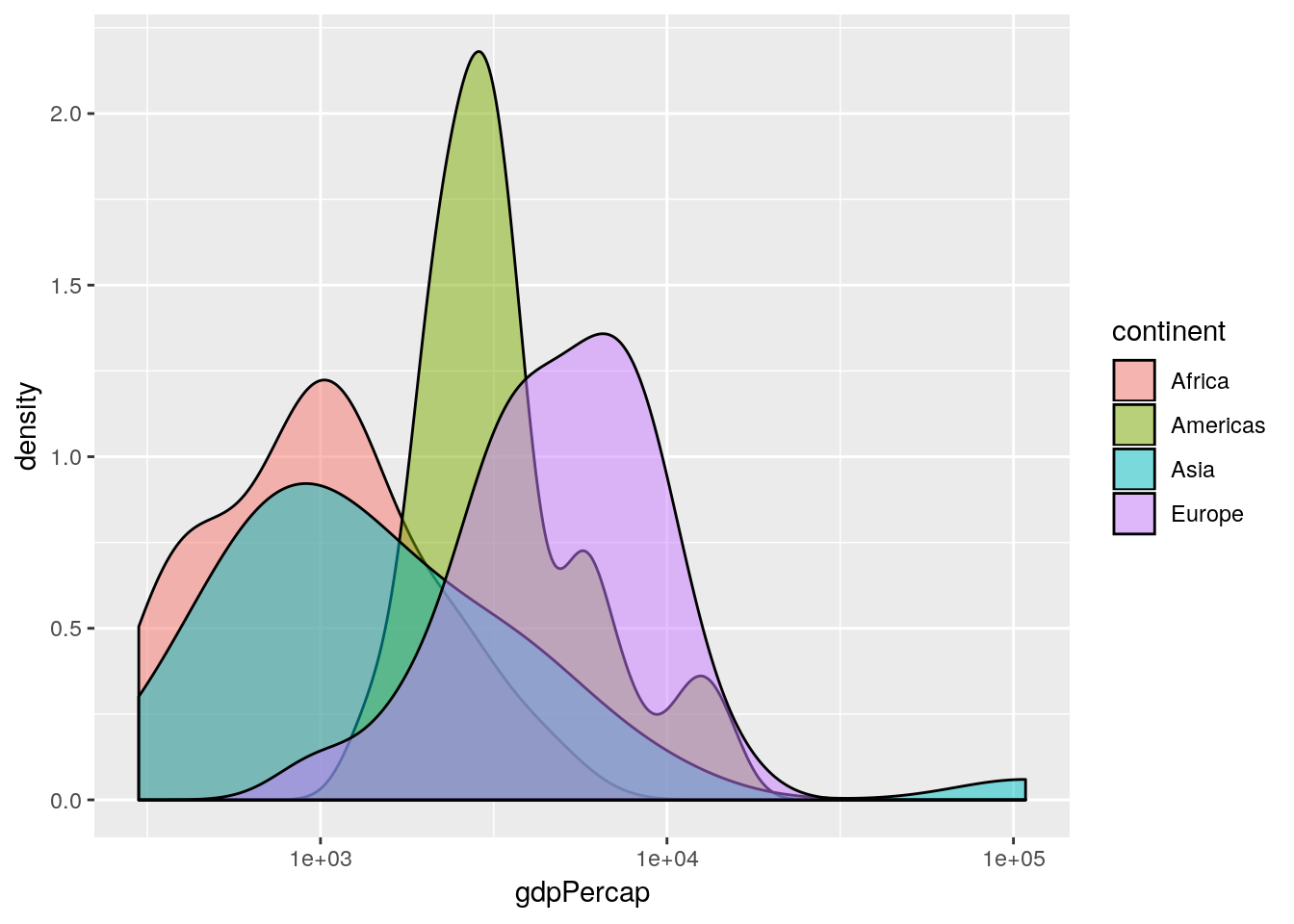

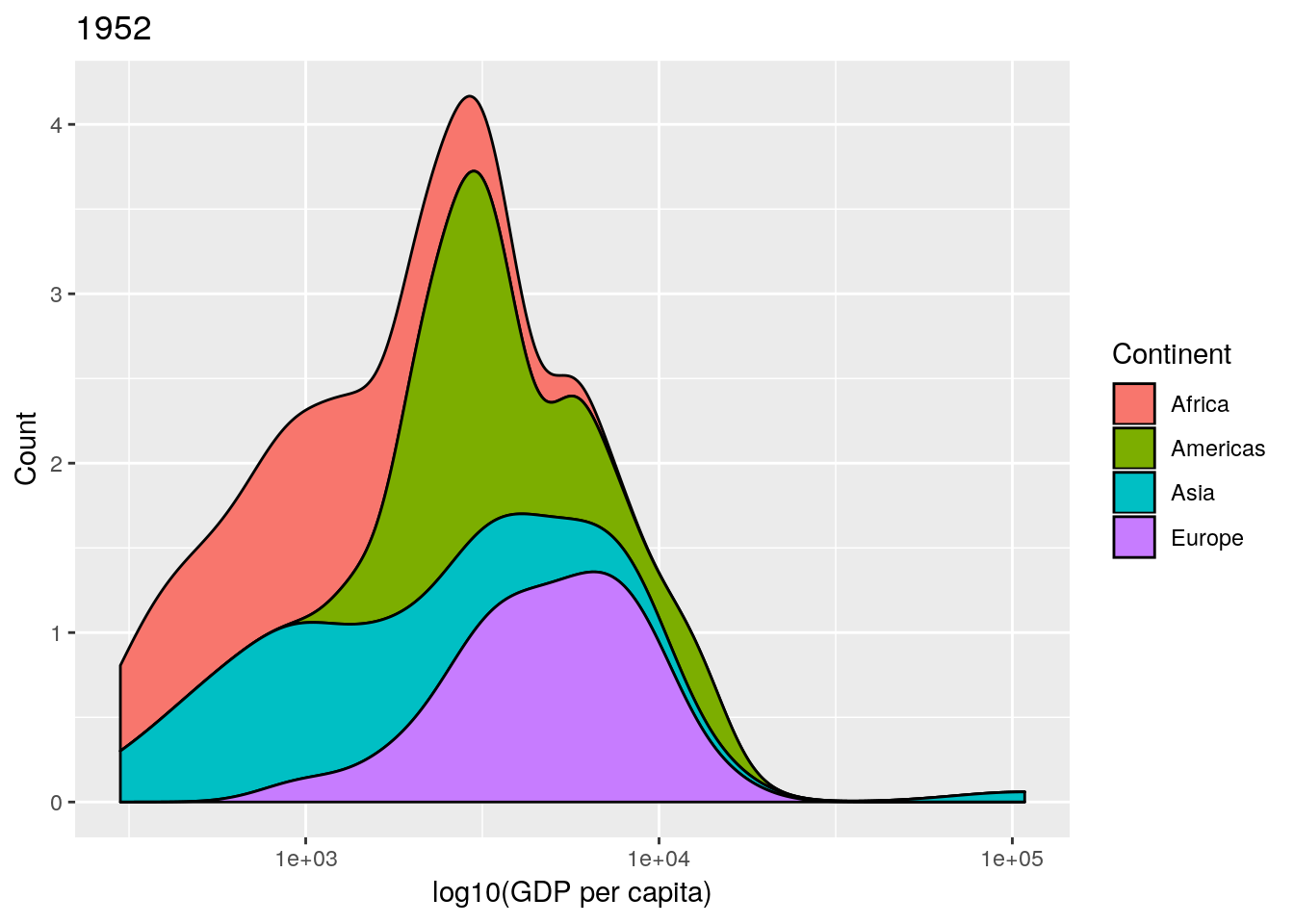
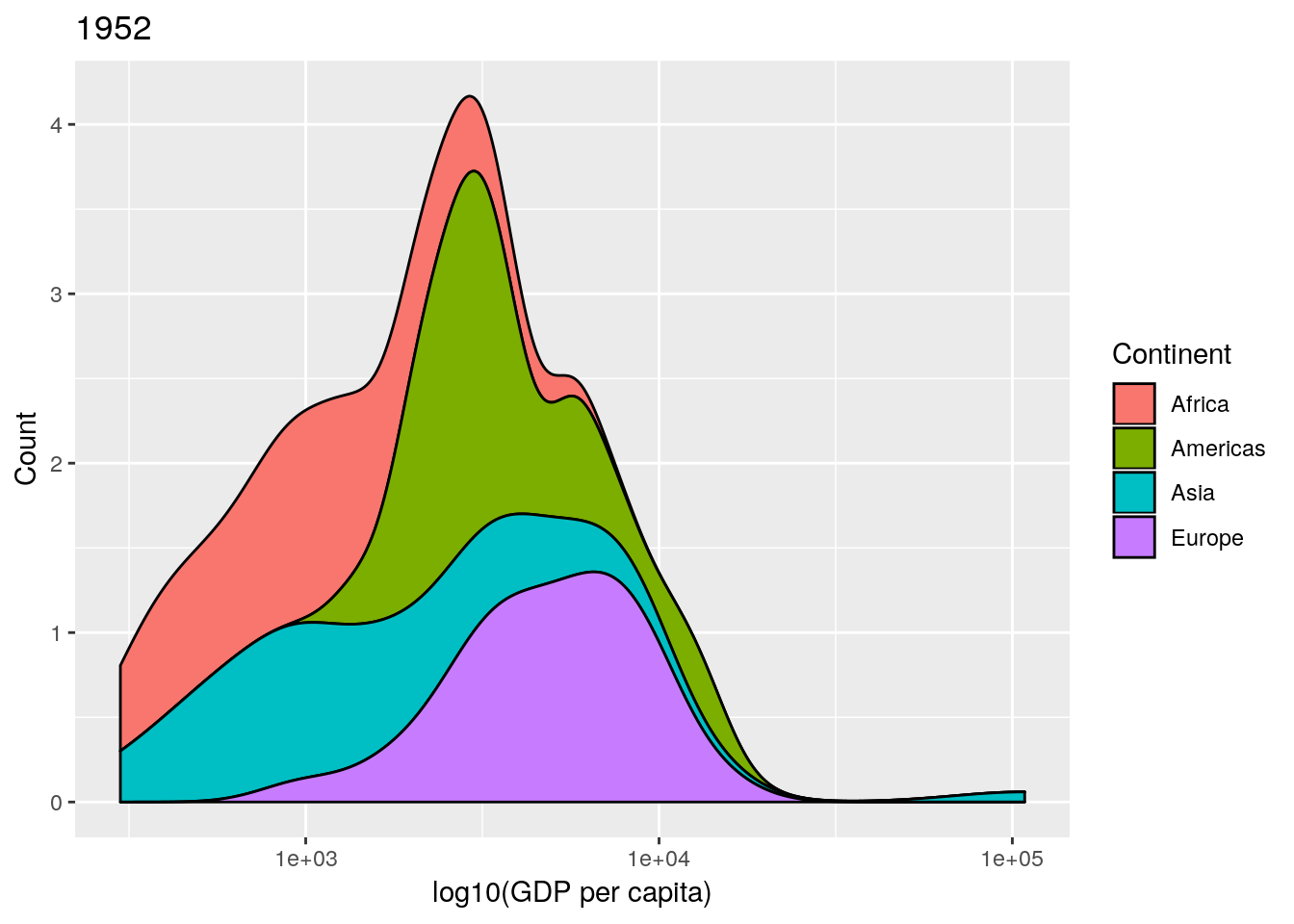
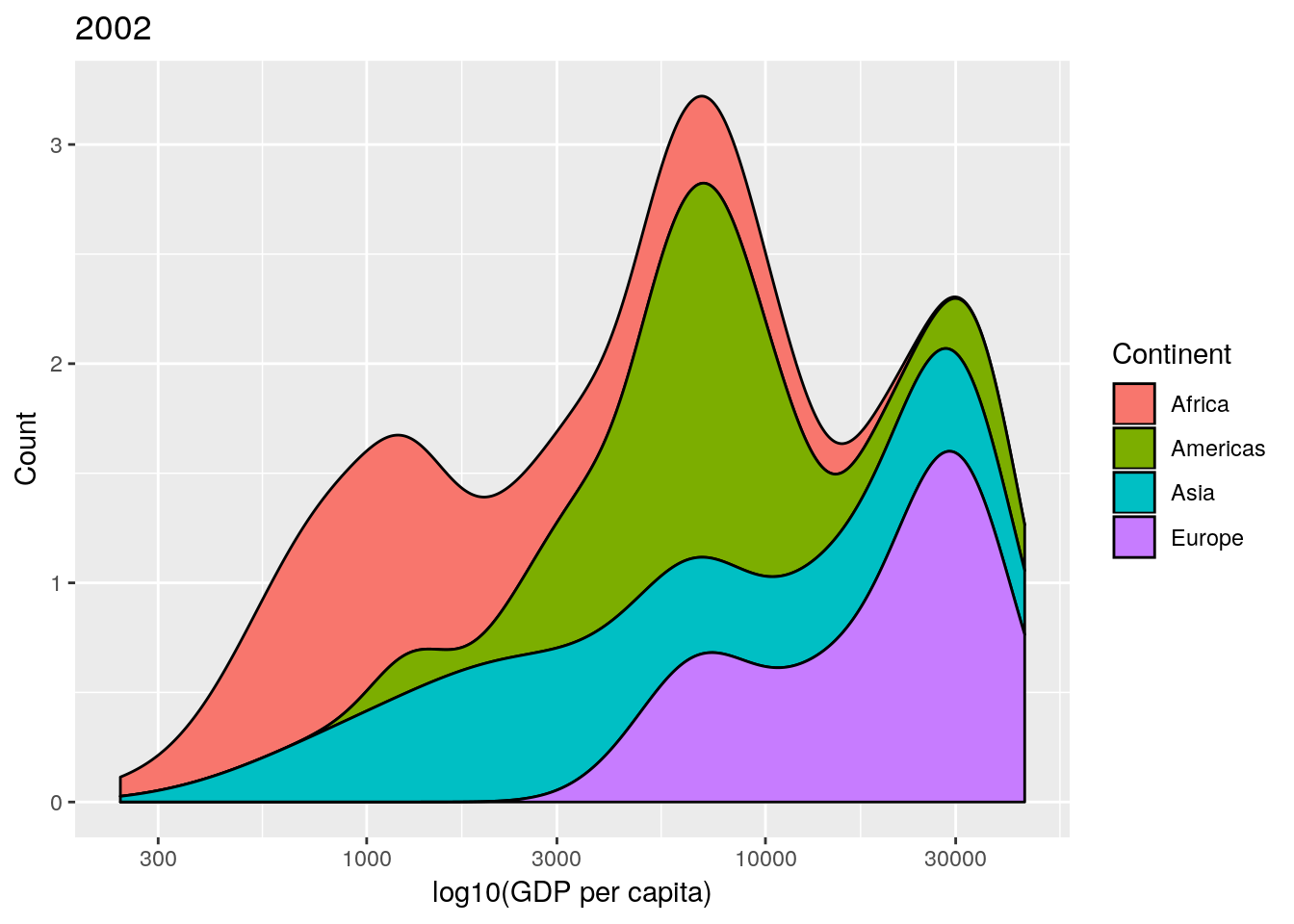
This is an informative plot. We can see that African countries tend to have lower GDP per capita than the Americas for example; with Asia and Africa the poorest continents in the 1950s in terms of GDP.

Aside: what does the Oceania density plot tell us about the range of GDPs in the Oceania continent?

1.4.2.1 Positions

Professor Rosling uses a stacked density plot, rather than overlapping density plots. We can use a position = "stack" argument to the geom to force the stacking.

## produce stacked density plot
ggplot(gapminderNoOc[gapminderNoOc$year == 1952, ],
       aes(x = gdpPercap, fill = continent)) +
    geom_density(position = "stack") +
    scale_x_log10()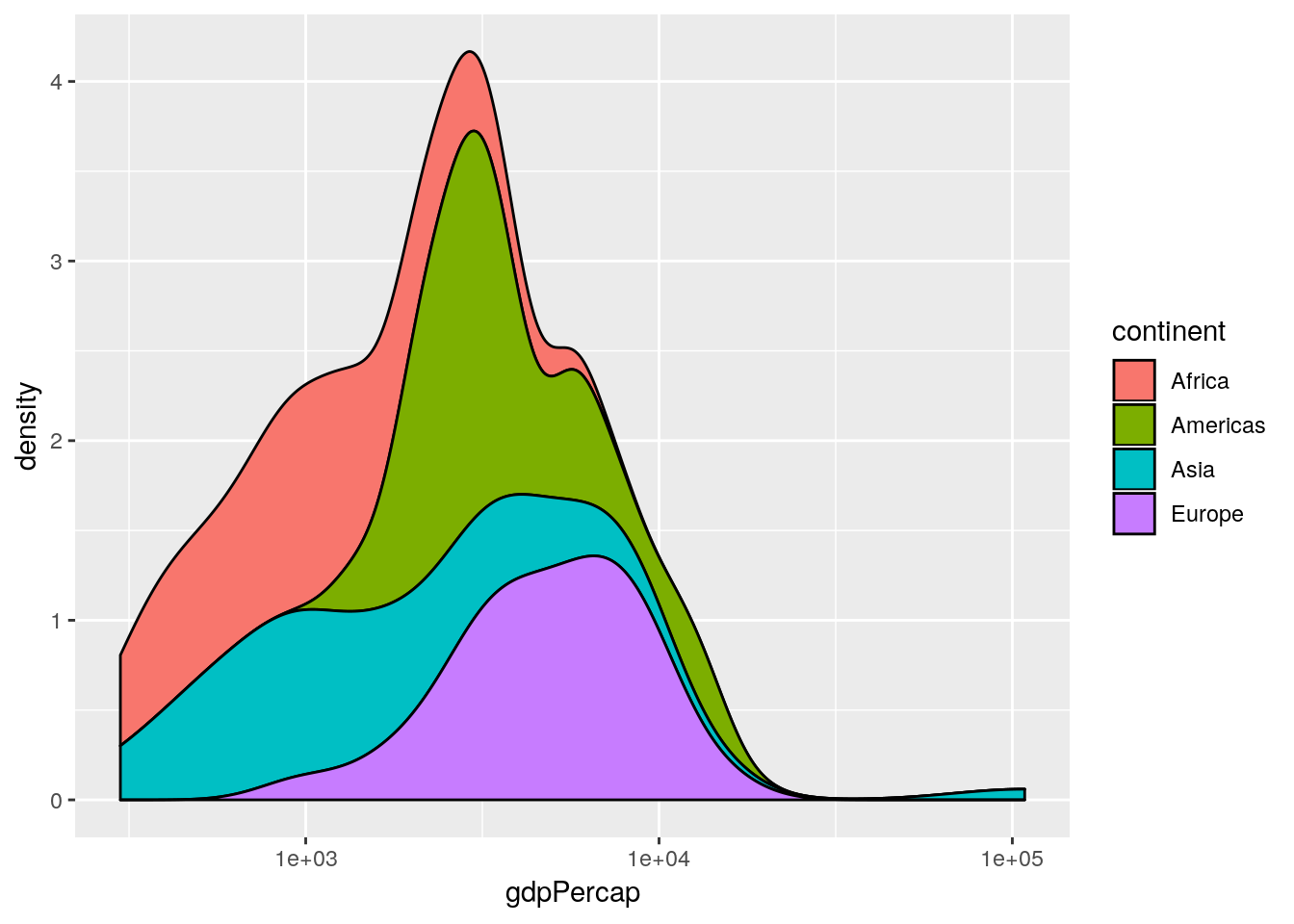 

Histograms and barplots have equivalent position = "dodge" and position = "stack" commands. By default histograms use the latter. The former is not very useful for histograms, but very useful for barplots with multiple discrete groupings.

Task

Try tidying up the axis and legend titles on these plots.

Solution

ggplot(gapminderNoOc[gapminderNoOc$year == 1952, ],
       aes(x = gdpPercap, fill = continent)) +
    geom_density(position = "stack") +
    scale_x_log10() +
    xlab("log10(GDP per capita)") + 
    ylab("Count") +
    ggtitle("1952") +
    labs(fill = "Continent")

Task

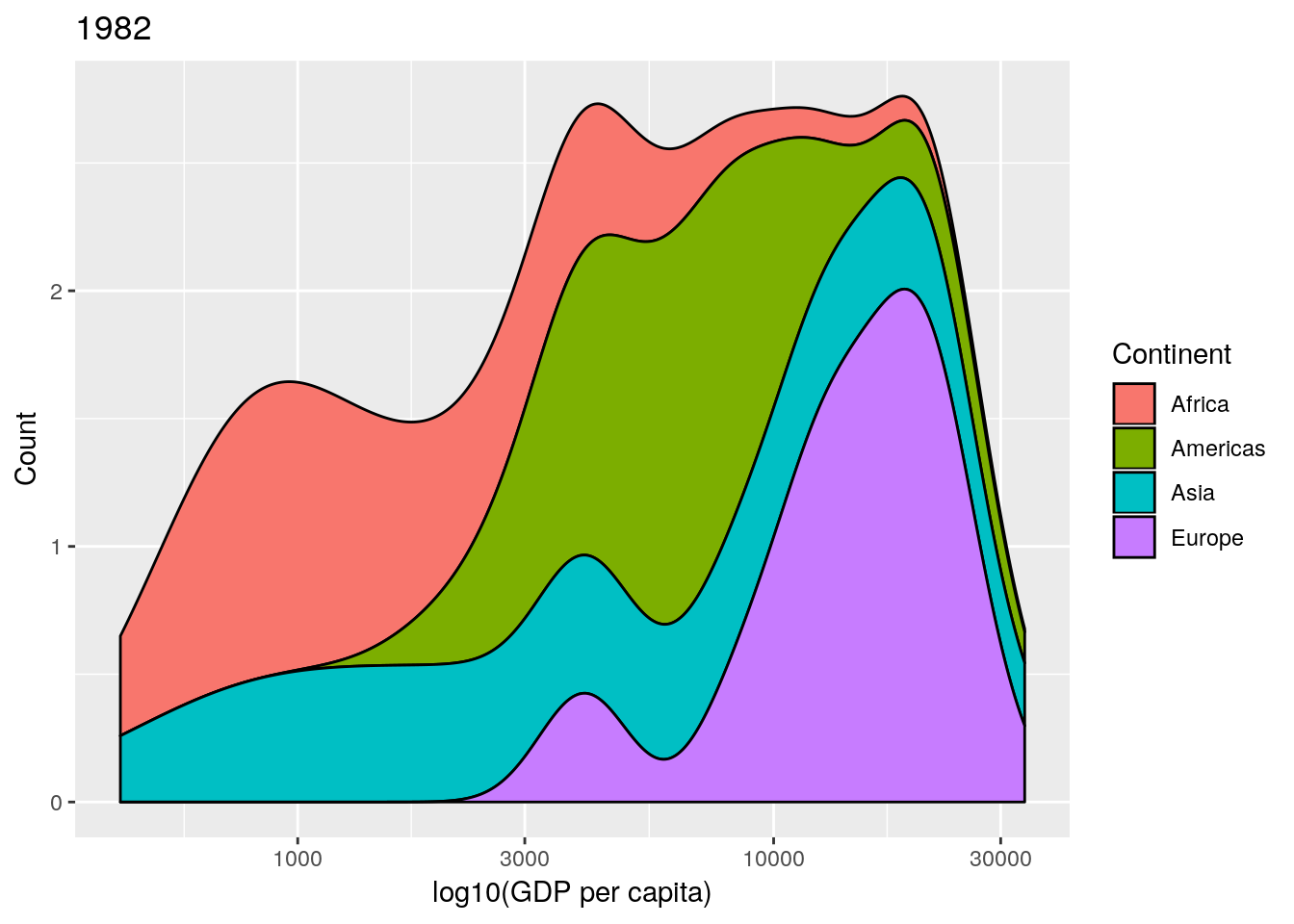
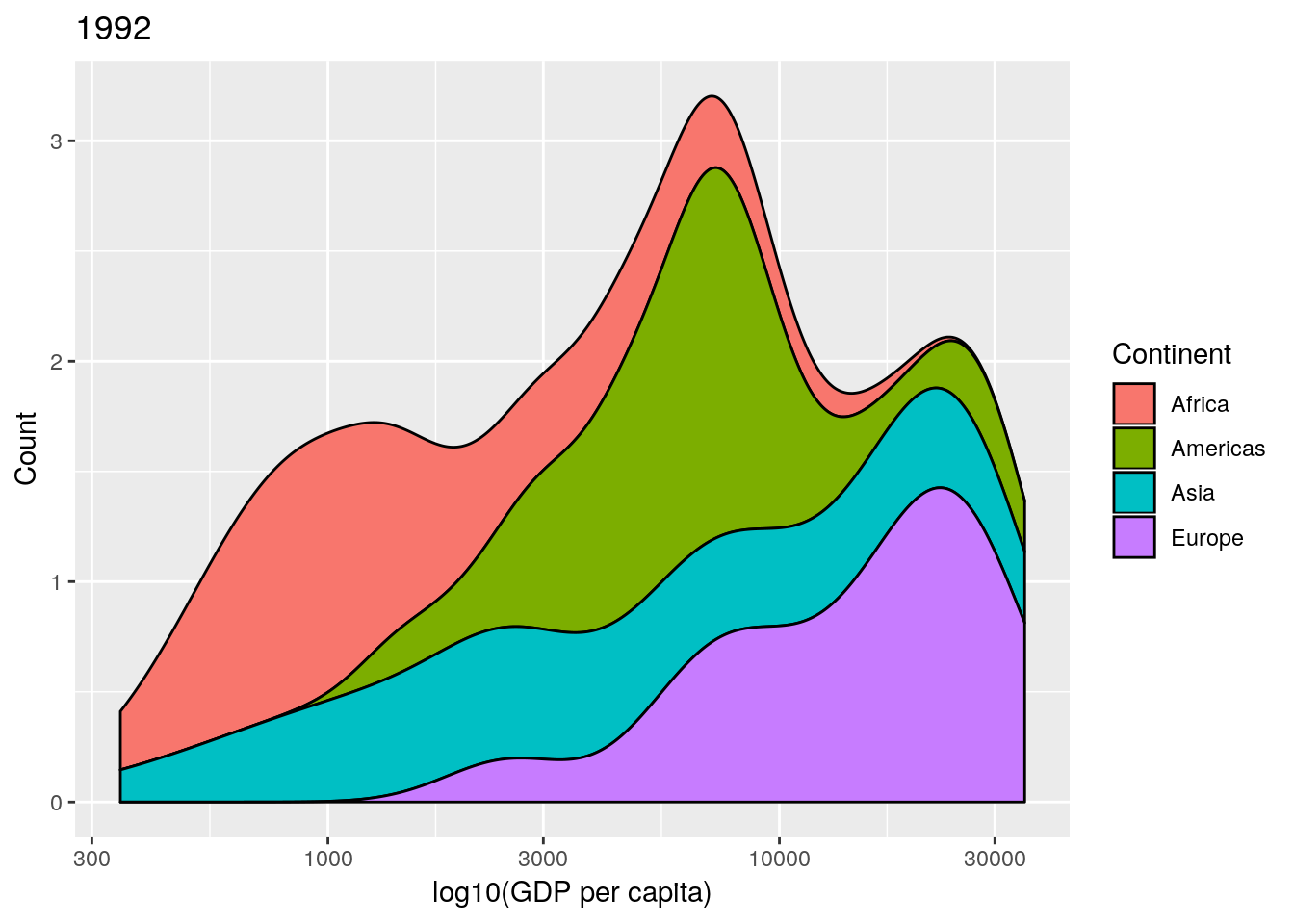
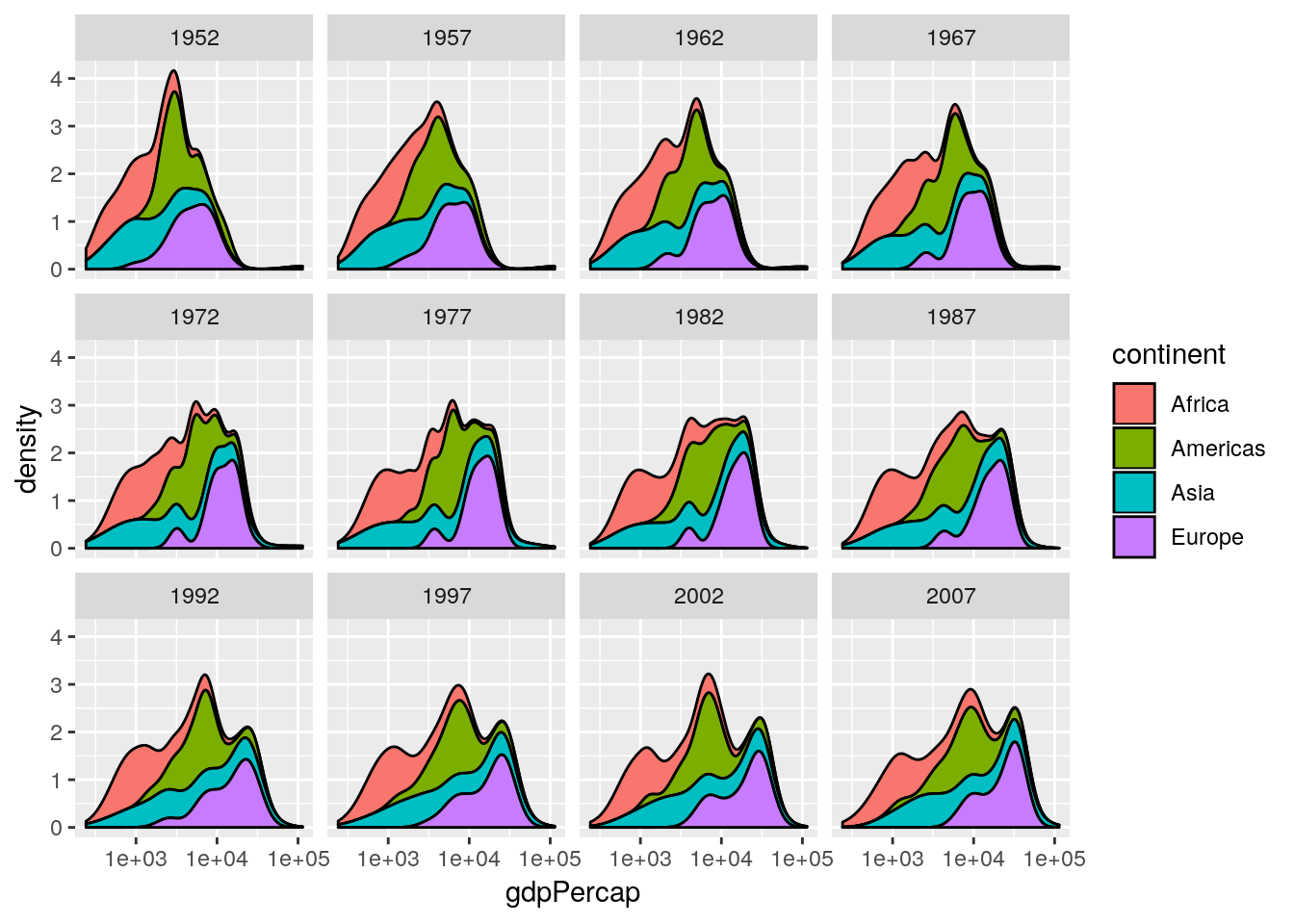
Write a function in R that takes a data and a year argument and plots a stacked density plot for a given year. Use this to plot the data for 1952, 1982, 1992 and 2002. (Remember that if you want to plot a ggplot2 figure from inside a function, you will have to call print() explicitly.)

Solution

plotGapminder_gg <- function(data, year) {
    p <- ggplot(data[data$year == year, ],
       aes(x = gdpPercap, fill = continent)) +
    geom_density(position = "stack") +
    scale_x_log10() +
    xlab("log10(GDP per capita)") + 
    ylab("Count") +
    ggtitle(year) +
    labs(fill = "Continent")
    print(p)
}
for(i in c(1952, 1982, 1992, 2002)) {
    plotGapminder_gg(gapminderNoOc, i)
}

Task

Produce a density plot of log10(gdpPercap) faceted by continent, for the year 1952.

Solution

ggplot(gapminderNoOc[gapminderNoOc$year == 1952, ],
       aes(x = gdpPercap)) +
    geom_density()  +
    scale_x_log10()  +
    facet_wrap(~ continent)

Task

Now generate a series of stacked density plots, with colours corresponding to different continents, but faceted by different years, to see how the relative distributions change over time.

Solution

ggplot(gapminderNoOc,
       aes(x = gdpPercap, fill = continent)) +
    geom_density(position = "stack") +
    scale_x_log10() +
    facet_wrap(~ year)

1.5 Additional task

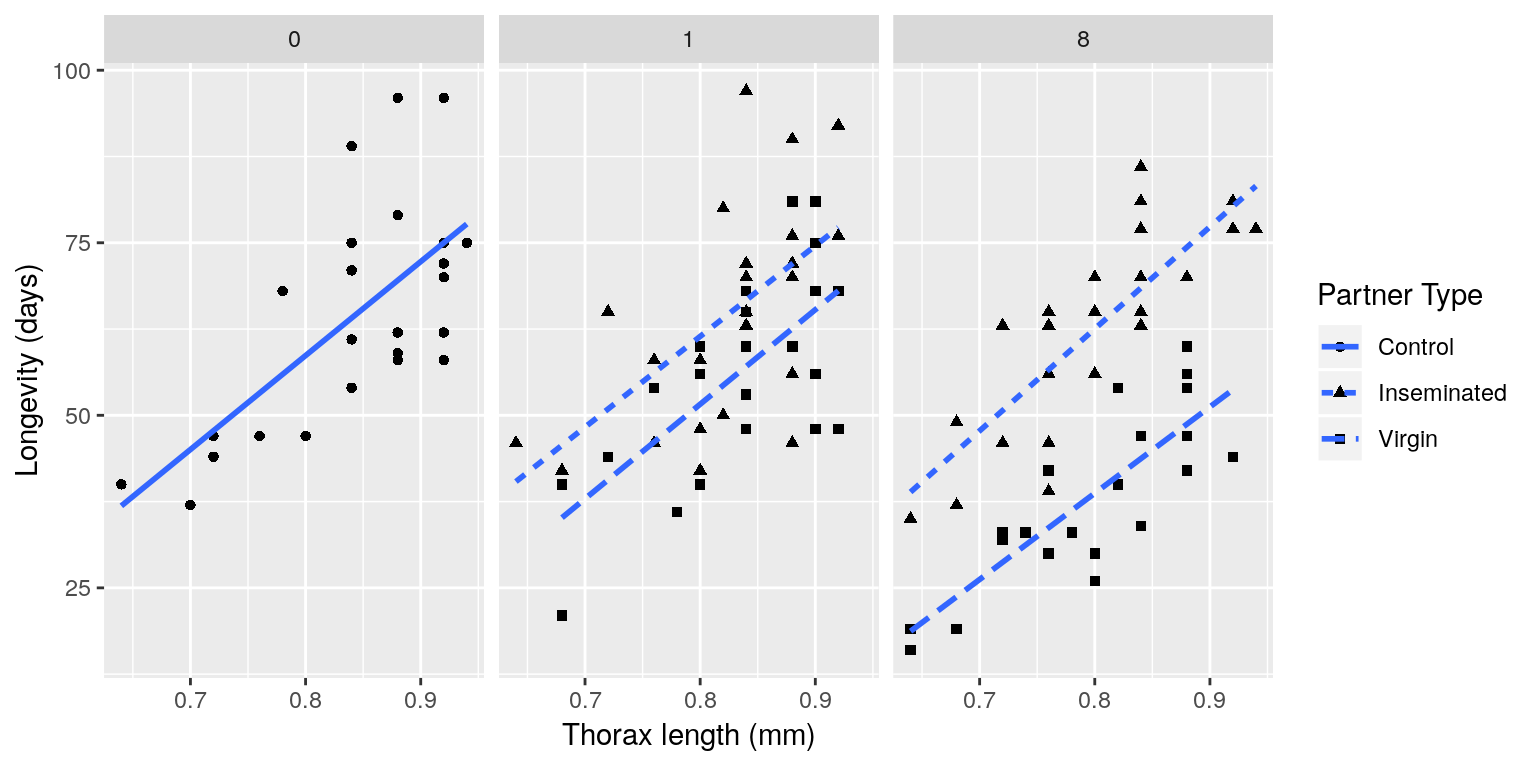
A cost of increased reproduction in terms of reduced longevity has been shown for female fruitflies, but not for males. We have data from an experiment that used a factorial design to assess whether increased sexual activity affected the lifespan of male fruitflies.

The flies used were an outbred stock. Sexual activity was manipulated by supplying individual males with one or eight receptive virgin females per day. The longevity of these males was compared with that of two control types. The first control consisted of two sets of individual males kept with one or eight newly inseminated females. Newly inseminated females will not usually remate for at least two days, and thus served as a control for any effect of competition with the male for food or space. The second control was a set of individual males kept with no females. There were 25 males in each of the five groups, which were treated identically in number of anaesthetizations (using \(\mathrm{CO}_2\)) and provision of fresh food medium.

The data should have the following columns:

• id: a ID for each fly in each group (1–25).
• partners: number of companions (0, 1 or 8).
• type: type of companion (inseminated female; virgin female; not applicable (when ‘partners = 0’)).
• longevity: lifespan, in days.
• thorax: length of thorax, in mm.

Source: Partridge and Farquhar (1981)

Task

The file “ff.rds” contains the data from this experiment. Download this data set to your working directory, read it into R using the command:

ff <- readRDS("ff.rds")

and use ggplot2 to reproduce something similar to the plot below:

.

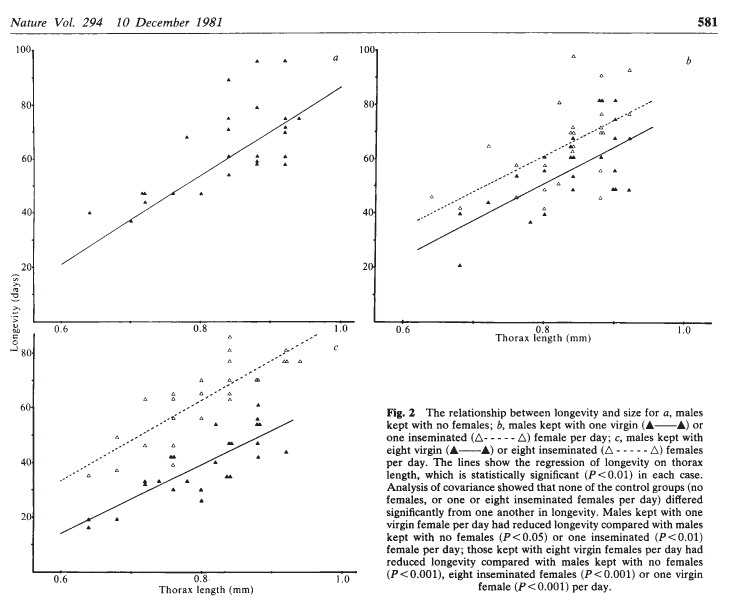Solution

## produce summary plot
ggplot(ff, aes(y = longevity, x = thorax, 
               linetype = type, shape = type)) +
    geom_point() +
    stat_smooth(method = "lm", se = F) +
    facet_wrap(~ partners) +
    labs(linetype = "Partner Type", shape = "Partner Type") +
    ylab("Longevity (days)") +
    xlab("Thorax length (mm)")

---

1. We will see tibble objects later on—just think of them as special data.frames.↩

2. just think of this as a smoothed line-of-best-fit through the data for the time being↩